The idea in all Bell inequalities is that you assume that the reason the particles give identical results whenever both experimenters measure the same property, even if they have a choice of which property to measure on each trial, is that the particles were created with identical "hidden" values for each possible property. Then, based on this assumption you can come up with some statistical statements about what you should see on trials where experimenters measure
different properties, giving a Bell inequality that tells you something about the statistics...then you can show that in QM the Bell inequality is violated, meaning that your original explanation for how the particles always give correlated results when the same property is measured must have been wrong, it can't simply be a matter of the two particles being created with identical hidden states.
The inequality used in the experiment above is known as the CHSH inequality. I showed the reasoning behind a different Bell inequality, in which there are three possible properties you can measure for each particle rather than two, in this post:
Suppose we have a machine that generates pairs of scratch lotto cards, each of which has three boxes that, when scratched, can reveal either a cherry or a lemon. We give one card to Alice and one to Bob, and each scratches only one of the three boxes. When we repeat this many times, we find that whenever they both pick the same box to scratch, they always get the same result--if Bob scratches box A and finds a cherry, and Alice scratches box A on her card, she's guaranteed to find a cherry too.
Classically, we might explain this by supposing that there is definitely either a cherry or a lemon in each box, even though we don't reveal it until we scratch it, and that the machine prints pairs of cards in such a way that the "hidden" fruit in a given box of one card always matches the hidden fruit in the same box of the other card. If we represent cherries as + and lemons as -, so that a B+ card would represent one where box B's hidden fruit is a cherry, then the classical assumption is that each card's +'s and -'s are the same as the other--if the first card was created with hidden fruits A+,B+,C-, then the other card must also have been created with the hidden fruits A+,B+,C-.
The problem is that if this were true, it would force you to the conclusion that on those trials where Alice and Bob picked different boxes to scratch, they should find the same fruit on at least 1/3 of the trials. For example, if we imagine Bob and Alice's cards each have the hidden fruits A+,B-,C+, then we can look at each possible way that Alice and Bob can randomly choose different boxes to scratch, and what the results would be:
Bob picks A, Alice picks B: opposite results (Bob gets a cherry, Alice gets a lemon)
Bob picks A, Alice picks C: same results (Bob gets a cherry, Alice gets a cherry)
Bob picks B, Alice picks A: opposite results (Bob gets a lemon, Alice gets a cherry)
Bob picks B, Alice picks C: opposite results (Bob gets a lemon, Alice gets a cherry)
Bob picks C, Alice picks A: same results (Bob gets a cherry, Alice gets a cherry)
Bob picks C, Alice picks picks B: opposite results (Bob gets a cherry, Alice gets a lemon)
In this case, you can see that in 1/3 of trials where they pick different boxes, they should get the same results. You'd get the same answer if you assumed any other preexisting state where there are two fruits of one type and one of the other, like A+,B+,C- or A+,B-,C-. On the other hand, if you assume a state where each card has the same fruit behind all three boxes, so either they're both getting A+,B+,C+ or they're both getting A-,B-,C-, then of course even if Alice and Bob pick different boxes to scratch they're guaranteed to get the same fruits with probability 1. So if you imagine that when multiple pairs of cards are generated by the machine, some fraction of pairs are created in inhomogoneous preexisting states like A+,B-,C- while other pairs are created in homogoneous preexisting states like A+,B+,C+, then the probability of getting the same fruits when you scratch different boxes should be somewhere between 1/3 and 1. 1/3 is the lower bound, though--even if 100% of all the pairs were created in inhomogoneous preexisting states, it wouldn't make sense for you to get the same answers in less than 1/3 of trials where you scratch different boxes, provided you assume that each card has such a preexisting state with "hidden fruits" in each box.
But now suppose Alice and Bob look at all the trials where they picked different boxes, and found that they only got the same fruits 1/4 of the time! That would be the violation of Bell's inequality, and something equivalent actually can happen when you measure the spin of entangled photons along one of three different possible axes. So in this example, it seems we can't resolve the mystery by just assuming the machine creates two cards with definite "hidden fruits" behind each box, such that the two cards always have the same fruits in a given box.
And you can modify this example to show some different Bell inequalities, see post #8 of
this thread for one example. As for the CHSH inequality, it's explained in the
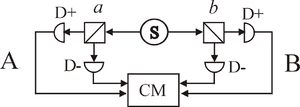
wikipedia article, but the proof may be a bit hard to follow there so I'll try to explain it in a step-by-step manner here. Instead of Alice and Bob having three boxes to scratch on their respective lotto cards, imagine they only have two boxes on their cards, and that we label Alice's two boxes a and a' while we label Bob's two boxes b and b'. When scratched, any given box will reveal either a cherry or a lemon. Once Alice and Bob have both found the fruit behind the box they choose, they can adopt the convention that a cherry is represented by a +1 and a lemon is represented by a -1, and multiply their respective numbers together to produce a single number for each trial (and that single number will itself be +1 if they both got the same fruit, and -1 if they got different fruits). Then we are interested in the "expectation value" for a given choice of boxes--for example, E(a,b') means the average result Alice and Bob will get after multiplying their numbers together on the subset of trials where Alice chose to scratch box a and Bob chose to scratch box b'. The CHSH inequality then states that if we define the value S by S=E(a,b) - E(a,b') + E(a',b) + E(a',b'), then -2 \leq S \leq 2.
As for the hidden states, there are 16 different possibilities (and here I am replacing each fruit with the number they've chosen to represent it, so a=+1 means that the hidden fruit in box a on Alice's card is a cherry):
1: a=+1, a'=+1, b=+1, b'=+1
2: a=+1, a'=+1, b=+1, b'=-1
3: a=+1, a'=+1, b=-1, b'=+1
4: a=+1, a'=+1, b=-1, b'=-1
5: a=+1, a'=-1, b=+1, b'=+1
6: a=+1, a'=-1, b=+1, b'=-1
7: a=+1, a'=-1, b=-1, b'=+1
8: a=+1, a'=-1, b=-1, b'=-1
9: a=-1, a'=+1, b=+1, b'=+1
10: a=-1, a'=+1, b=+1, b'=-1
11: a=-1, a'=+1, b=-1, b'=+1
12: a=-1, a'=+1, b=-1, b'=-1
13: a=-1, a'=-1, b=+1, b'=+1
14: a=-1, a'=-1, b=+1, b'=-1
15: a=-1, a'=-1, b=-1, b'=+1
16: a=-1, a'=-1, b=-1, b'=-1
In this case, define something like A(a,12) to mean "the value Alice gets if she picks a and the hidden state of the two cards is 12", so going by the above we'd have A(a,12)=-1. Similarly B(b',7)=+1, and so forth. And we can assume that there must be well-defined probabilities for each of the possible hidden states, which can be represented with notation like p(8) and p(15) etc.
Since the expectation value E(a,b) is the
average value Alice and Bob get when they multiply their results together in the subset of trials where Alice picks box a and Bob picks box b, we should have: E(a,b) = \sum_{N=1}^{16} A(a,N)*B(b,N)*p(N). Likewise, we should also have E(a,b') = \sum_{N=1}^{16} A(a,N)*B(b',N)*p(N). Combining these gives:
E(a,b) - E(a,b') = \sum_{N=1}^{16} [A(a,N)*B(b,N) - A(a,N)*B(b',N)]*p(N)
With a little creative algebra you can see the above can be rewritten as:
E(a,b) - E(a,b') = \sum_{N=1}^{16} A(a,N)*B(b,N)*[1 \pm A(a',N)*B(b',N)]*p(N) <br />
- \sum_{N=1}^{16} A(a,N)*B(b',N)*[1 \pm A(a',N)*B(b,N)]*p(N)
The
triangle inequality says that for any real numbers x and y, |x + y| \leq |x| + |y|, so applying this to the above gives:
|E(a,b) - E(a,b')| \leq | \sum_{N=1}^{16} A(a,N)*B(b,N)*[1 \pm A(a',N)*B(b',N)]*p(N) | + | \sum_{N=1}^{16} A(a,N)*B(b',N)*[1 \pm A(a',N)*B(b,N)]*p(N) |
The triangle inequality also implies that the absolute value of a sum of terms is less than or equal to the sum of the absolute value of each term, so this gives:
|E(a,b) - E(a,b')| \leq \sum_{N=1}^{16} |A(a,N)*B(b,N)*[1 \pm A(a',N)*B(b',N)]*p(N)| + \sum_{N=1}^{16} |A(a,N)*B(b',N)*[1 \pm A(a',N)*B(b,N)]*p(N)|
Since A(a,N)*B(b,N) is either +1 or -1, and so is A(a,N)*B(b',N), then we can remove them without affecting the absolute value of each term, giving:
|E(a,b) - E(a,b')| \leq \sum_{N=1}^{16} |[1 \pm A(a',N)*B(b',N)]*p(N)| + \sum_{N=1}^{16} |[1 \pm A(a',N)*B(b,N)]*p(N)|
Since A(a',N)*B(b',N) must be either +1 or -1, [1 ± A(a',N)*B(b',N)] must always be non-negative, and likewise for [1 ± A(a',N)*B(b,N)]. And each p(N) is a probability, so p(N) must always be non-negative too. This means the absolute values on the right side of the equation are unnecessary, so we have:
|E(a,b) - E(a,b')| \leq \sum_{N=1}^{16} [1 \pm A(a',N)*B(b',N)]*p(N) + \sum_{N=1}^{16} [1 \pm A(a',N)*B(b,N)]*p(N)
Since \sum (x ± y) = \sum x + \sum ± y, we can rewrite that as:
|E(a,b) - E(a,b')| \leq \sum_{N=1}^{16} p(N) + \sum_{N=1}^{16} \pm [A(a',N)*B(b',N)]*p(N) + \sum_{N=1}^{16} p(N) + \sum_{N=1}^{16} \pm [A(a',N)*B(b,N)]*p(N)
And since there are 16 possible hidden states, it must be true that \sum_{N=1}^{16} p(N) = 1, so:
|E(a,b) - E(a,b')| \leq 2 + \sum_{N=1}^{16} \pm [A(a',N)*B(b',N)]*p(N) + \sum_{N=1}^{16} \pm [A(a',N)*B(b,N)]*p(N)
And by the definition of the expectation values, this reduces to:
|E(a,b) - E(a,b')| \leq 2 ± [E(a',b') + E(a',b)]
Or:
|E(a,b) - E(a,b')| ± [E(a',b') + E(a',b)] \leq 2
which implies
|E(a,b) - E(a,b')| + |E(a',b') + E(a',b)| \leq 2
And again using the triangle inequality we get:
|E(a,b) - E(a,b') + E(a',b') + E(a',b)| \leq 2
...which is just the CHSH inequality. So this shows that if we assume there is a definite hidden state for the four boxes on the two cards given to Alice and Bob on each trial, then no matter what the probabilities of different possible hidden states (different possible combinations of fruits behind the four boxes), we'd expect this inequality to be respected. If the inequality is violated as in quantum mechanics, that means that picturing their measurements as just revealing preexisting hidden states cannot be correct.