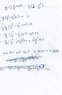\frac{}{}
Sadeq said:
Thank you very much.
I uploaded two pictures the first one is regarding the first question and the second one is regarding the second.
You can zoom them to see more clearly.
Appreciate your help ,to better understanding.
Thank you again
The two pages you posted were helpful, and I may be able to answer your questions to some extent, but some information is still lacking.
I see by the chapter title in the page corner, that these questions refer to the bending of a thin circular plate. Therefore, I presume in these expressions, \ r\,,\ is the radial coordinate in a cylindrical coordinate system. ... etc. ...
Anyone helping you with such a problem, shouldn't be expected to be digging such information out, just to help you. You should be supplying such information.
I can only hazard a guess as to what \ \alpha\ represents. I see that \ W\ is a quantity referred to as deflection and is related to \ \alpha\ by \displaystyle \ \alpha=\frac{dW}{dr}\ .
At any rate, my earlier post in this thread was pretty much on the mark regarding Question 1 . \ W\ is defined only on the disc, r ≤ R .
The quantity, \displaystyle \ \ W=\frac{Fr^2}{16\pi D}\left(2\ln\left(\frac{r}{R}\right)-1+\left(\frac{R}{r}\right)^2\, \right)\,, \ has a removable discontinuity at r = 0 (the origin). It may be helpful to graph W as a function of r. To aid you in doing that, let u = r/R, then r = R∙u . This gives you
\displaystyle \ \ W=\frac{FR^2}{16\pi D}u^2\left(2\ln\left(u\right)-1+\frac{1}{u^2}\, \right)\ . \
So you can actually graph the u dependence of this function. Where is its maximum? \ W\ is defined only on the disc, r ≤ R , so in terms of u, it's only defined for |u| ≤ 1.
What is \displaystyle \ \ \frac{dW}{dr}\ ?