Lipd
Nevermind, I was able to solve it.
---
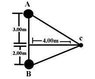
Two small speakers emit spherical sound waves of different frequencies. Speaker A has an output of 1.00 mW and speaker B has an output of 1.50 mW. Determine the sound level (in decibels) at point C if a) only speaker A emits sound, b)only speaker B emits sound, c) both speakers emit sound.
The attachment has the distances and arrangement of the speakers and the point c.
Any help is much appreciated, thanks!
---
Two small speakers emit spherical sound waves of different frequencies. Speaker A has an output of 1.00 mW and speaker B has an output of 1.50 mW. Determine the sound level (in decibels) at point C if a) only speaker A emits sound, b)only speaker B emits sound, c) both speakers emit sound.
The attachment has the distances and arrangement of the speakers and the point c.
Any help is much appreciated, thanks!
Attachments
Last edited by a moderator: