dekoi
edit // 1-4 have been answered. Please scroll down.
-----
Firstly, i would like to make sure whether i am clear on this subject.
If A is (2, 3, 5) and B (5, 2, -3), would AB equal (3, -1, -8) ? And the magnitude of AB would be the Square.root(9+1+64+ .
Either way, i would like someone to assist me in these problems.
1.) "Find the components of the unit vector with direction opposite to that of the vector from X(7,4,-2) to Y(1,2,1)
I first figured out XY, which is (6, -2, 3). Am i correct to assume the opposite of this XY is (-6, 2, -3) ? I then used the formula for the unit vector calculation to figure out the coordinates of the unit vector.However, my answer was (-6/7, 2/7, -3/7) -- while the correct answer should be (6/7, 2/7, 3/7).
2.) ABCDEF is a regular hexagon with sides of unit length. Find the magnitude of direction of AB + AC + AD + AE + AF (all vectors). ABCDEF is drawn counter-clockwise (for conveniance).
I first made AF = AB. Therefore, 2AB + AC +AD + AE. Then AE = AC. Therefore, 2AB + 2AC + AD. Now, am i correct to say AD = AB + BC + CD ? The rest i should be able to calculate.
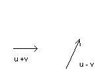
3.) The sum and the difference of two vectors u and v are given. Show how to find the vectors themselves.
See attached image for Diagram.
I am completely stuck on this one. Is there a proper way of doing it, without trial and error?
4.) Find the length of the median AM in the triangle ABC, for the points A (2, 3/2, -4), B (3, -4, 2), and C (1, 3, -7).
Once again, would e.g AB equal x2 - x1, y2-y1, z2-z1 ?
Thank you.
Please repond asap.
-----
Firstly, i would like to make sure whether i am clear on this subject.
If A is (2, 3, 5) and B (5, 2, -3), would AB equal (3, -1, -8) ? And the magnitude of AB would be the Square.root(9+1+64+ .
Either way, i would like someone to assist me in these problems.
1.) "Find the components of the unit vector with direction opposite to that of the vector from X(7,4,-2) to Y(1,2,1)
I first figured out XY, which is (6, -2, 3). Am i correct to assume the opposite of this XY is (-6, 2, -3) ? I then used the formula for the unit vector calculation to figure out the coordinates of the unit vector.However, my answer was (-6/7, 2/7, -3/7) -- while the correct answer should be (6/7, 2/7, 3/7).
2.) ABCDEF is a regular hexagon with sides of unit length. Find the magnitude of direction of AB + AC + AD + AE + AF (all vectors). ABCDEF is drawn counter-clockwise (for conveniance).
I first made AF = AB. Therefore, 2AB + AC +AD + AE. Then AE = AC. Therefore, 2AB + 2AC + AD. Now, am i correct to say AD = AB + BC + CD ? The rest i should be able to calculate.
3.) The sum and the difference of two vectors u and v are given. Show how to find the vectors themselves.
See attached image for Diagram.
I am completely stuck on this one. Is there a proper way of doing it, without trial and error?
4.) Find the length of the median AM in the triangle ABC, for the points A (2, 3/2, -4), B (3, -4, 2), and C (1, 3, -7).
Once again, would e.g AB equal x2 - x1, y2-y1, z2-z1 ?
Thank you.
Please repond asap.
Attachments
Last edited by a moderator: