- #1
denfaro
- 8
- 2
Hi I am a beginner in this topic. I didn't understand this question type clearly.What does it mean" With Magnitude and Unit Vectors" exactly? May you help me for the solution step by step :). Thanks in advance.
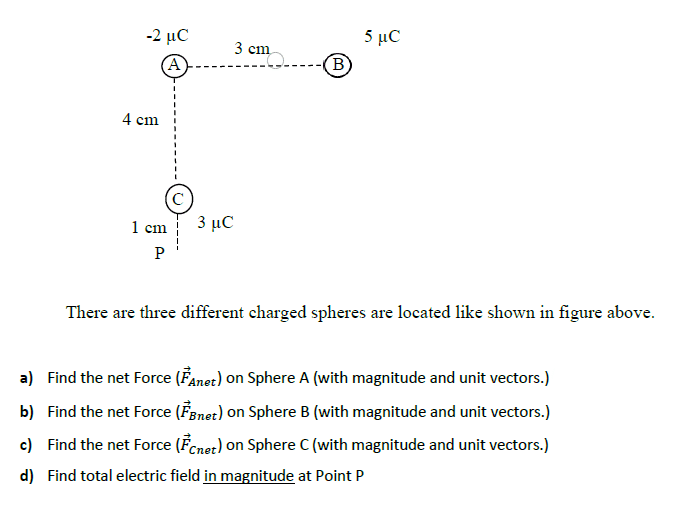
Welcome to the PF.denfaro said:Hi I am a beginner in this topic. I didn't understand this question type clearly.What does it mean" With Magnitude and Unit Vectors" exactly? May you help me for the solution step by step :). Thanks in advance.
View attachment 260846
Yes I learned the vectors,coordinate system but I don't know how can I use them on this question.berkeman said:Welcome to the PF.
Your thread has been moved to the Schoolwork forums.
We cannot do your schoolwork/homework for you, but perhaps we can give you a few tips to help your understanding so that you can start working on the problem.
What have you done with vectors so far? You know that vectors have a magnitude and direction, right? And have you learned about coordinate systems like Caretesian coordinates, where there are x and y directions, etc.?
So start by drawing an x-y set of axes on the diagram. I would probably make the (0,0) point at the A charge, with the x-axis to the right and the y-axis pointing up.denfaro said:Yes I learned the vectors,coordinate system but I don't know how can I use them on this question.
Do you know charged spheres will apply force on each other?denfaro said:Yes I learned the vectors,coordinate system but I don't know how can I use them on this question.
Yes I knowAdesh said:Do you know charged spheres will apply force on each other?
What’s the expression for that force? I mean is there any law which governs how two charged spheres will apply force on each other ?denfaro said:Yes I know
I think you mean Coulmb's LawAdesh said:What’s the expression for that force? I mean is there any law which governs how two charged spheres will apply force on each other ?
Yes. Can you please write out the Coulombs Law?denfaro said:I think you mean Coulmb's Law
F=(k*(q1*q2))/r^2.Adesh said:Yes. Can you please write out the Coulombs Law?
But force is a vector quantity, the expression which you have given doesn’t involve the direction of the force. Can you fix it? Can you do something so that we get a vector quantity in that expression of Coulombs Law?denfaro said:F=(k*(q1*q2))/r^2.
Sorry I don't. How can I do that?Adesh said:But force is a vector quantity, the expression which you have given doesn’t involve the direction of the force. Can you fix it? Can you do something so that we get a vector quantity in that expression of Coulombs Law?
$$\vec{F} = k \frac{q_1 ~q_2 }{r^2}~ \hat{r}$$ the force acts on the line joining the two charges.denfaro said:Sorry I don't. How can I do that?
Thanks I have an idea now. :)Adesh said:$$\vec{F} = k \frac{q_1 ~q_2 }{r^2}~ \hat{r}$$ the force acts on the line joining the two charges.
A magnitude vector is a mathematical representation of a vector's length or size. It is typically denoted by ||v||, where v is the vector, and is calculated using the Pythagorean theorem.
A unit vector is a vector that has a magnitude of 1 and is used to represent direction. It is typically denoted by a hat symbol (^) over the vector, such as â or ı̂. Unit vectors are important in vector calculations as they help to determine direction and can be used to scale other vectors.
The magnitude of a vector can be found using the Pythagorean theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. In vector terms, this means that the magnitude of a vector ||v|| can be calculated as √(v1² + v2² + v3²), where v1, v2, and v3 are the components of the vector in each dimension.
To find the unit vector of a given vector, you first need to find the magnitude of the vector using the Pythagorean theorem. Then, divide each component of the vector by the magnitude to get the unit vector. For example, if the given vector is v = (3, 4, 5), the magnitude is √(3² + 4² + 5²) = √50. The unit vector would then be (3/√50, 4/√50, 5/√50).
Magnitude and unit vectors are used in many areas of physics and engineering, such as mechanics, electromagnetism, and fluid dynamics. They are used to represent physical quantities, such as force, velocity, and acceleration, and to perform calculations involving these quantities. In engineering, they are used to design and analyze structures and systems, such as bridges, buildings, and electrical circuits.