shalini.singh
- 1
- 0
My problem is like this:
I have a 2 dimensional domain
Now, that domain is made up of eleemnts- these elemnts are triangular
or quadrilateral in shape. Each triangualr and quadrilateral element has 3 and 4 vertices (a triangular element has 3 vertices and quadrilateral has 4 vertices).
We have fixed function values at these vertices- the function is (Say) F
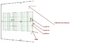
In that 2-D domain we define a strip (a strip is just a part of the area of that domain), A strip may have several sections - (those) lines as in attached figure (summary-figure.jpg)- the vertical lines are sections.
What I need is::
I need to integrate the resultant (function) along the length of each design strip section and
hence across the width of the design strip.
I could think to proceed in the following steps::
The inputs are:
A) All the triangle/quadrilateral vertices
B) Function values at all the vertices
C) The line over which you want to integrate
D)geometry of the strip
The broad algorithm would be like this:
1. Find which quadrilaterals/triangles this line intersects
2. Find the function values at the points of intersection of the line with the sides of these quadrilatrals/triangles
3. Use numerical integration to integrate the function from these values
Can anyone help me with a better algorithm?
Also, how would I proceed with 3 above?What would be the best for numerical integration?
Someone suggested about Chebyshev polynomials- but I do not have any idea of it!
Please please can anyone help?It si very urgent
Shalini
I have a 2 dimensional domain
Now, that domain is made up of eleemnts- these elemnts are triangular
or quadrilateral in shape. Each triangualr and quadrilateral element has 3 and 4 vertices (a triangular element has 3 vertices and quadrilateral has 4 vertices).
We have fixed function values at these vertices- the function is (Say) F
In that 2-D domain we define a strip (a strip is just a part of the area of that domain), A strip may have several sections - (those) lines as in attached figure (summary-figure.jpg)- the vertical lines are sections.
What I need is::
I need to integrate the resultant (function) along the length of each design strip section and
hence across the width of the design strip.
I could think to proceed in the following steps::
The inputs are:
A) All the triangle/quadrilateral vertices
B) Function values at all the vertices
C) The line over which you want to integrate
D)geometry of the strip
The broad algorithm would be like this:
1. Find which quadrilaterals/triangles this line intersects
2. Find the function values at the points of intersection of the line with the sides of these quadrilatrals/triangles
3. Use numerical integration to integrate the function from these values
Can anyone help me with a better algorithm?
Also, how would I proceed with 3 above?What would be the best for numerical integration?
Someone suggested about Chebyshev polynomials- but I do not have any idea of it!
Please please can anyone help?It si very urgent
Shalini