hawkslime
- 2
- 0
- TL;DR Summary
- Can someone give me an explanation of the below picture, please?
Hello, I was glazing through what I would consider an advanced physics textbook and I saw this image. It is a schematic picture of an alpha-particle in a field of an atom.
Now, can someone get me started on what (and why and how) is going on in it? Especially with the fraction with pi.
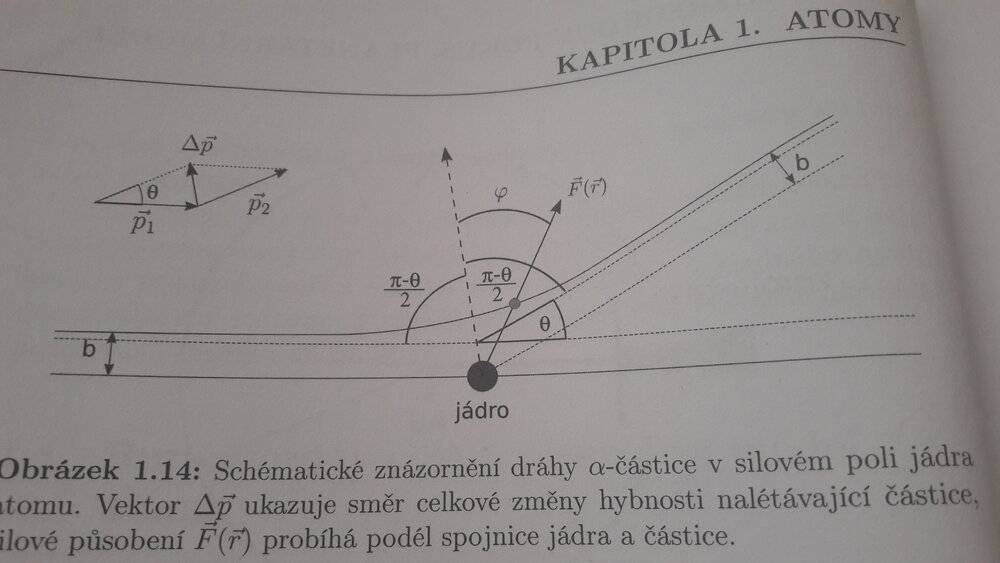
Now, can someone get me started on what (and why and how) is going on in it? Especially with the fraction with pi.