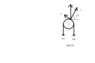Amin2014
- 114
- 3
Consider a massless string which can rotate about a fixed pulley (first picture). The coefficient of static friction is μ. Assuming that the motion is impending, the goal is to find the equation that describes the variation in tension of the string.
( T2/T1 = eμΦ where Φ is the subtended angle.)
The usual method of solving this problem involves writing Newton's law for an infinitesimal element of the string and then integrating. In the second picture I've provided an extract from a different problem. Why can't we apply the solution provided in the second picture to the original problem stated above?
( T2/T1 = eμΦ where Φ is the subtended angle.)
The usual method of solving this problem involves writing Newton's law for an infinitesimal element of the string and then integrating. In the second picture I've provided an extract from a different problem. Why can't we apply the solution provided in the second picture to the original problem stated above?