etf
- 179
- 2
Hi!
Here is my task:
1. Homework Statement
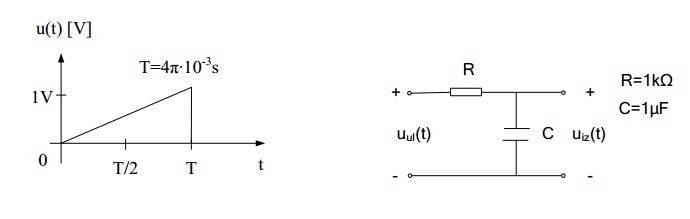
Periodic signal is input signal for circuit (photo).
a) Calculate and sketch amplitude spectrum of $$u(t+1ms)$$,
b) Calculate participation (in percent) of DC component of power of total mean power of signal $$u(t)$$,
c) Sketch power spectrum of signal $$u1(t)=u(t)-1V$$
d) Calculate power of third harmonic on output
[/B]
I represented $$u(t)$$ in terms of complex Fourier series as $$u(t)=\frac{E}{2}+\sum_{n=-\infty ,n\neq 0}^{n=\infty }F_ne^{jnw0t},$$ where $$F_n=\frac{E}{2n\pi }j,$$ $$T=4\pi *10^{-3}s,$$ $$w0=\frac{2\pi }{4\pi *10^{-3}},$$ $$E=1V.$$ Then I used time shift property of Fourier series to represent $$u(t+1ms)$$. I got $$u(t+1ms)=\frac{E}{2}+\sum_{n=-\infty,n\neq 0}^{n=\infty}F_ne^{-jnw0*0.001}e^{jnw0t}$$ ($$F_n$$ is same as for $$u(t)$$. Then I sketch it so task a) is completed. For task b) I calculated total mean power of signal as (if it's correct) $$P=\lim_{t->\infty}\frac{1}{T}\int_{\tau}^{\tau+T}(f(t))^{2}dt=\lim_{t->\infty}\frac{1}{T}\int_{\tau}^{\tau+T}(\frac{Et}{T})^{2}dt=...=\frac{E^{2}}{3}=\frac{1}{3}$$. What would be participation in percent of DC component? How to do other tasks?
Here is my task:
1. Homework Statement
Periodic signal is input signal for circuit (photo).
a) Calculate and sketch amplitude spectrum of $$u(t+1ms)$$,
b) Calculate participation (in percent) of DC component of power of total mean power of signal $$u(t)$$,
c) Sketch power spectrum of signal $$u1(t)=u(t)-1V$$
d) Calculate power of third harmonic on output
Homework Equations
The Attempt at a Solution
[/B]
I represented $$u(t)$$ in terms of complex Fourier series as $$u(t)=\frac{E}{2}+\sum_{n=-\infty ,n\neq 0}^{n=\infty }F_ne^{jnw0t},$$ where $$F_n=\frac{E}{2n\pi }j,$$ $$T=4\pi *10^{-3}s,$$ $$w0=\frac{2\pi }{4\pi *10^{-3}},$$ $$E=1V.$$ Then I used time shift property of Fourier series to represent $$u(t+1ms)$$. I got $$u(t+1ms)=\frac{E}{2}+\sum_{n=-\infty,n\neq 0}^{n=\infty}F_ne^{-jnw0*0.001}e^{jnw0t}$$ ($$F_n$$ is same as for $$u(t)$$. Then I sketch it so task a) is completed. For task b) I calculated total mean power of signal as (if it's correct) $$P=\lim_{t->\infty}\frac{1}{T}\int_{\tau}^{\tau+T}(f(t))^{2}dt=\lim_{t->\infty}\frac{1}{T}\int_{\tau}^{\tau+T}(\frac{Et}{T})^{2}dt=...=\frac{E^{2}}{3}=\frac{1}{3}$$. What would be participation in percent of DC component? How to do other tasks?
Last edited: