Buns_of_Steel
- 4
- 0
Hi guys,
I'm new here and this is my first post so apologies if its in the wrong location or anything.
My post is not in regards to a direct question as such but i am more looking for general advice and guidance on how to tackle a problem. I am working on a project that involves lifting equipment to pick up an object.
One of the components is a clamping arm with a single pivot point shown below.
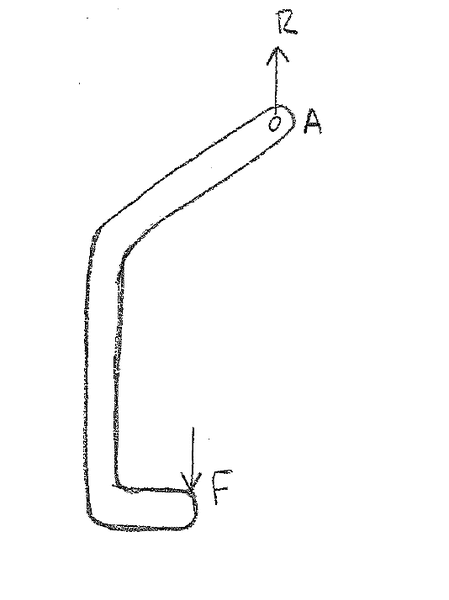
The arm is constant width and constant thickness and the shape is approximately what is shown ie the point load F will cause counter clockwise rotation of the lever arm about point A.
What i need assistance with is how calculate the maximum deflection, maximum direct and shear stresses and what the relevant equations are. How do i go about breaking the problem down into manageable chunks?
Dimensions and forces are not important as it is the principles of how to calculate stresses etc which i am looking for.
Any help would be great. Let me know if you need any more info.
Cheers
I'm new here and this is my first post so apologies if its in the wrong location or anything.
My post is not in regards to a direct question as such but i am more looking for general advice and guidance on how to tackle a problem. I am working on a project that involves lifting equipment to pick up an object.
One of the components is a clamping arm with a single pivot point shown below.
The arm is constant width and constant thickness and the shape is approximately what is shown ie the point load F will cause counter clockwise rotation of the lever arm about point A.
What i need assistance with is how calculate the maximum deflection, maximum direct and shear stresses and what the relevant equations are. How do i go about breaking the problem down into manageable chunks?
Dimensions and forces are not important as it is the principles of how to calculate stresses etc which i am looking for.
Any help would be great. Let me know if you need any more info.
Cheers