loreberto911
- 4
- 0
< Mentor Note -- thread moved to HH from the technical engineering forums, so no HH Template is shown >[/color]
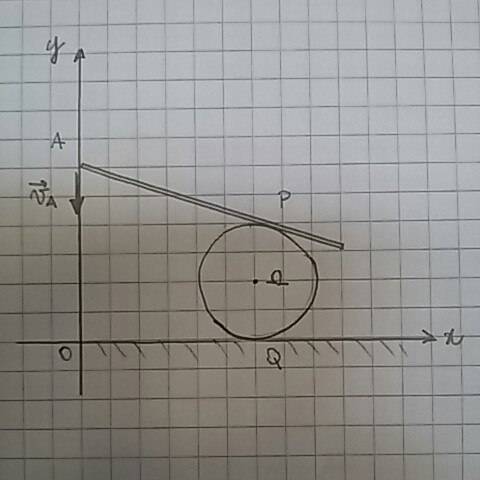
A rod rolls without creep. And the disk rolls without creep on Q. The rod can just moves on y. Which is the relation among Va and Vohm?
Va= velocity in A
My resolution:
in Q we know that velocity is zero.Q is also the instant rotation center ( disk).so the P point ( disk) is the fastest. How to bound speed in
##\Omega## and Va?
I mean, just seeing the picture, without using the fondant formula of rigid cinematic. I could think it's like the half of Va.
Ps.it's my first article and my english isn't so good, I hope you'll understand anyway.
A rod rolls without creep. And the disk rolls without creep on Q. The rod can just moves on y. Which is the relation among Va and Vohm?
Va= velocity in A
My resolution:
in Q we know that velocity is zero.Q is also the instant rotation center ( disk).so the P point ( disk) is the fastest. How to bound speed in
##\Omega## and Va?
I mean, just seeing the picture, without using the fondant formula of rigid cinematic. I could think it's like the half of Va.
Ps.it's my first article and my english isn't so good, I hope you'll understand anyway.
Attachments
Last edited by a moderator: