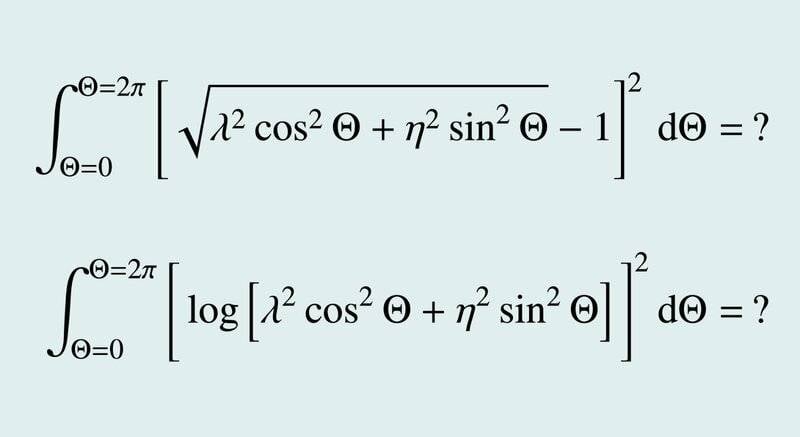SUMMARY
This discussion focuses on finding analytical solutions for integrals in polar coordinates, specifically the integral -2 ∫ √(λ² cos²θ + η² sin²θ) dθ. The constants λ and η are positive and less than 10. The integrand can be expressed as a Taylor series for cases where λ > η and λ < η, facilitating integration. Additionally, the last integral resembles a multiple of the complete elliptic integral of the second kind, which may provide an analytical solution if special functions are considered.
PREREQUISITES
- Understanding of polar coordinates and their applications in calculus.
- Familiarity with Taylor series expansions and their integration.
- Knowledge of complete elliptic integrals and their properties.
- Basic proficiency in integral calculus involving square roots of trigonometric functions.
NEXT STEPS
- Research the properties and applications of complete elliptic integrals of the second kind.
- Study Taylor series expansions for trigonometric functions in detail.
- Explore analytical solutions for integrals involving square roots of trigonometric expressions.
- Investigate the use of special functions in solving complex integrals.
USEFUL FOR
Mathematicians, physicists, and engineers involved in advanced calculus, particularly those working with integrals in polar coordinates and seeking analytical solutions.