Analyzing an Oscillating Slingshot System

[GreenLantern674]

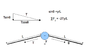
A ball of mass m is connected to two rubber bands of length, L, each under tension T, as in Figure P12.49. The ball is displaced by a small distance y perpendicular to the length of the rubber bands.

(a) Assuming that the tension does not change, show that the restoring force is -2yT/L .
(b) Assuming that the tension does not change, show that the system exhibits simple harmonic motion with an angular frequency .

I have no idea how to solve this. I think it has something to do with F=ma, but I don't know exactly what.

Help?

 

[rl.bhat]

There is no figure in the quote. What is the angle between the two rubber band?

 

[Shooting Star]

Hi GreenLantern674,

Let's call the direction in which the displacement has been made the positive y-axis, and let the initial length of the bands lie along the x-axis.

After the displacement y, the rubber bands each make an angle theta with the x-axis.

Now, resolve the components of each of the tensions T along the y-axis and the x-axis. The horizontal tensions are each Tcos(theta) and balance each other. The y-component of each of the tension T is Tsin(theta). So, the force acting on the particle is 2Tsin(theta) towards the origin. Then we can write,

md^2y/dt^2 = -2Tsin(theta). From the right-angled triangle, sin(theta) = y/L. So,

md^y/dt^2 = -2Ty/L. This force acts toward the original position and so is a restoring force.

For the 2nd question, tell me in which situations do you encounter this first eqn. Go through your notes or books and tell me the rest of the answer.

 

[GreenLantern674]

I've never seen that kind of equation before, except in the equation A=[F/m]/(sqrt(w2 - (k/m)2) , which turns into something kinda similar when you solve for w.

Also, what is the "d" in md^y/dt^2 = -2Ty/L?

 

[Shooting Star]

> Also, what is the "d" in md^y/dt^2 = -2Ty/L

That's a very obvious typo. It should read md^2y/dt^2 = -2Ty/L, which means,

ma = -2Ty/L, where the accn a is given by d^2y/dt^2.

The eqn of SHM is ma = -kx.

Have you studied SHM and how to find omega from the eqn?

 

[cepheid]

Ok, here's how I'm envisioning the problem:

http://img89.imageshack.us/img89/2307/tensionde4.th.png

This picture is attached as well.

Part a is fairly simple, if you look at the vector diagram, you can see that the downward component of the tension force from EACH rubber band is given by -Tsin(theta), where sin(theta) = y/L (which should be clear from the geometry in the figure.

Then, in the vertical direction, Newton's second law becomes:

ma_y = -2Ty/L

Shooting star is using calculus to write this as:

m \frac{d^2 y}{dt^2} = -2T\frac{y}{L}

Where the symbol \frac{d^2}{dt^2} should be taken to be one whole symbol that is being applied to y, and it means "take the second dervative of y with respect to time." If you don't know what that means, don't worry about it. This is the differential equation of a simple harmonic oscillator, but I don't think your teacher intended for you to use differential equations to solve for it. So, given that you have a RESTORING FORCE i.e. our equation is of the general form:

ma_y = -ky

where k is some constant, it seems pretty clear that we'll get oscillation. What rules has your teacher taught you about deducing the frequency of oscillation (omega) using this type of equation as a starting point?

 

[Shooting Star]

In my last post, I've said that the eqn for SHM is ma = -kx. If the OP has at all done SHM, it can't get clearer than that. I don't think he has studied it.

 

[GreenLantern674]

I know that max acceleration equals Aw^2 and we've used the formula a=Aw^2 cos(wt+phi)

 

[Shooting Star]

Where does the maximum accn happen in SHM? Or, in other words, what is the max amplitude in this problem? Imediately, you'll get omega.

 

[GreenLantern674]

Also, the problem defines L as the horizontal aspect of the triangle. Can I use the small angle theorum to assume that the hypotenuse is the same as the horizontal component?

 

[Shooting Star]

Not necessary.

In an SHM, the eqn is ma = -kx. So, if you can reduce the eqn to this form, we immediately know that it must be SHM. The omega = sqrt(k/m).

We have already shown that the eqn is ma = -(2T/L)y, where y is the displacement. Then omega should be sqrt(m/(2T/L) = sqrt(2mL/T). Note that T has been given as a const.

 

[Shooting Star]

A typo again! The omega should be sqrt(k/m) = sqrt(2T/(Lm)). Sorry for that.