Analyzing the Oscillation of a Plank on a Log

[Jahnavi]

Homework Statement

Homework Equations

The Attempt at a Solution

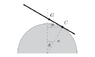
C is the point of contact and G is the CM of the plank . x be the distance between G and C .Since plank always remain in contact , x=aθ

When the line joining the point of contact C with the center makes an angle θ with the vertical ,the force due to gravity mg acts vertically down and exerts a torque about the point of contact C.

Torque due to Mg = Mgxcosθ

Since θ is small , cosθ ≈ 1 and using x=aθ

Mgxcosθ ≈ Mgaθ

Moment of inertia about C = M(2b)²/12 + Mx² =Mb²/3+Ma²θ²

Since θ is small , θ²≈0

Moment of inertia about C = Mb²/3

Writing torque equation about C ,

-Mgaθ = (Mb²/3)α ( α is angular acceleration )

α = -3gaθ/b²

Angular frequency of oscillation ω = √(3ga)(1/b)

Time period = 2π/ω = 2πb/√(3ga)

Is my work correct ?

 

[haruspex]

correct ?

Looks good.

 

[Jahnavi]

Thanks !