Shirish
- 242
- 32
I'm watching this minutephysics video on Lorentz transformations (part starting from 2:13 and ending at 4:10). In my spacetime diagram, my worldline will be along the ##ct## axis and the worldline of an observer moving relative to me will be at some angle w.r.t. the ##y## axis.
When we switch to the other observer's spacetime diagram, the observer's worldline will be along the ##y## axis and my worldline would flip over to the other side, but the angle between the worldlines would be preserved. Then the video goes on to mention three possibilities:
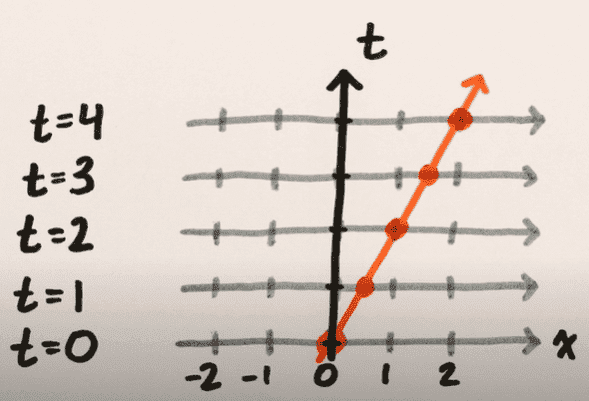
The event at ##(2,4)## ends up getting mapped to ##(0,T)##, where ##T<4##, ##T=4## or ##T>4##. And it seems like the video is suggesting only one possible transformation for each case, giving a total of only three possible transformations. For an angle preserving transformation ##A##, given any two unit vectors ##u_1,u_2##, $$[u_1]^TM[u_2]=[u_1]^TA^TMA[u_2]\implies M=A^TMA$$ where ##M## is the metric we're assuming for the space. Seems like (though I'm not a 100% sure) the ##T>4## possibility corresponds to rotation (Euclidean, sure about this one), ##T=4## to Galilean boost (Galilean) and ##T<4## to Lorentz boost (Minkowski metric).
But why is it being suggested that only these three transformations (satisfying the angle preservation and linearity properties) are possible? Is it possible to find any other transformations than rotation for the case of ##T>4##, or other than Lorentz for ##T<4##, etc.? If not, can anyone direct me to a proof or explanation of why only three transformations are possible?
(Specifically a mathematical argument/proof of why Euclidean, Galilean and Lorentz must be the only linear angle-preserving transformations in flat geometry would be nice)
When we switch to the other observer's spacetime diagram, the observer's worldline will be along the ##y## axis and my worldline would flip over to the other side, but the angle between the worldlines would be preserved. Then the video goes on to mention three possibilities:
The event at ##(2,4)## ends up getting mapped to ##(0,T)##, where ##T<4##, ##T=4## or ##T>4##. And it seems like the video is suggesting only one possible transformation for each case, giving a total of only three possible transformations. For an angle preserving transformation ##A##, given any two unit vectors ##u_1,u_2##, $$[u_1]^TM[u_2]=[u_1]^TA^TMA[u_2]\implies M=A^TMA$$ where ##M## is the metric we're assuming for the space. Seems like (though I'm not a 100% sure) the ##T>4## possibility corresponds to rotation (Euclidean, sure about this one), ##T=4## to Galilean boost (Galilean) and ##T<4## to Lorentz boost (Minkowski metric).
But why is it being suggested that only these three transformations (satisfying the angle preservation and linearity properties) are possible? Is it possible to find any other transformations than rotation for the case of ##T>4##, or other than Lorentz for ##T<4##, etc.? If not, can anyone direct me to a proof or explanation of why only three transformations are possible?
(Specifically a mathematical argument/proof of why Euclidean, Galilean and Lorentz must be the only linear angle-preserving transformations in flat geometry would be nice)