Angle to Shoot Bow & Arrow at Object 1m Deep in Lake

  • Thread starter jumbogala
  • Start date
  • Tags
    Refraction
In summary, the man's eyes make an angle of 30 degrees below the horizontal as he looks at the treasure chest at the bottom of the lake. To shoot the chest with a bow and arrow, he must aim at an angle of 60 degrees with respect to a vertical normal. The law of refraction, nisin(θi) = nrsin(θr), can be used to find the angle of incidence (θi) by substituting in the values of n1 = 1 and n2 = 1.33. The height of the man's eyes above the ground and the depth of the lake are not necessary in solving this problem.
  • #1
jumbogala
423
4

Homework Statement


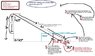
A man whose eyes are 2 m above the ground is looking into a clear lake. He sees a treasure chest on the bottom of the lake, which is 1 m deep. His eyes make an angle of 30 degrees below the horizontal as he looks at the chest.

If he wants to shoot the chest with a bow and arrow (so he can pull it to the surface), at what angle should he shoot the arrow?

State the angle with respect to the horizontal.

Homework Equations


I learned the law of refraction was nisin(θi) = nrsin(θr). The angle is with respect to a VERTICAL normal. so \| the angle between those two lines is the angle of the ray going in, |\ that's the angle going out.

i means incidient, r means refracted.


The Attempt at a Solution


I can't get an answer for this, but I'm not sure what I'm doing wrong.

I'm assuming that when the guy is looking at the object, he's seeing the refracted object. The real object is actually in a different spot. So the angle that his eyes make with respect to the vertical should be θr.

If the guy's eyes make an angle of 30 degrees from the horizontal, then the angle with respect to a vertical normal must be 60 degrees.

Then using the equation given I should be able to solve for θi. But I can't, because it gives sin-1 > 1, which is impossible.

Also, I didn't use the heights given to me at all and I think I'm supposed to. What am I doing wrong?
 
Physics news on Phys.org
  • #2
You must have mixed up the substitution into the refraction formula. On your diagram, label the air side 1 and write n1 = 1. On the water side 2, n2 = 1.33. Show your formula with numbers if you need more help!
 
  • #3
Check out this amaturistic diagram, hope it helps?:confused:
 

Attachments

  • defraction ratio.jpg
    defraction ratio.jpg
    46.2 KB · Views: 398
  • #4
Please tell me is this anywhere close?
 
  • #5
No one can see your attachment until it is approved.
It would be quicker if you uploaded it to a photo site like photobucket.com and then posted a link here. If you put IMG and /IMG (both in square brackets) around the link, the image will appear right in the post.
 

FAQ: Angle to Shoot Bow & Arrow at Object 1m Deep in Lake

What is the optimal angle to shoot a bow and arrow at an object 1m deep in a lake?

The optimal angle to shoot a bow and arrow at an object 1m deep in a lake depends on several factors such as the depth of the lake, the distance from the shore, and the type of bow and arrow being used. Generally, a 45-degree angle is recommended for shooting into water as it allows for maximum accuracy and distance.

How does the depth of the lake affect the angle needed to shoot a bow and arrow at an object?

The depth of the lake affects the angle needed to shoot a bow and arrow at an object because the deeper the water, the higher the angle needed to ensure the arrow reaches the desired target. This is due to the resistance of the water, which can slow down the arrow's speed and trajectory.

What are the different factors that can affect the angle needed to shoot a bow and arrow at an object in a lake?

Aside from the depth of the lake, other factors that can affect the angle needed to shoot a bow and arrow at an object include wind speed and direction, the weight and type of the arrow, and the skill level of the archer. These factors should be taken into account when determining the optimal shooting angle.

Is there a specific technique for shooting a bow and arrow at an object in a lake?

Yes, there are specific techniques for shooting a bow and arrow at an object in a lake. These techniques include adjusting the angle of the bow, using a lighter arrow to compensate for water resistance, and aiming slightly higher than the intended target to account for the arrow's trajectory in the water.

What safety precautions should be taken when shooting a bow and arrow at an object in a lake?

When shooting a bow and arrow at an object in a lake, it is important to ensure that the surrounding area is clear of any people or objects. It is also crucial to have a clear line of sight to the target and to never aim the arrow at a person or animal. Additionally, proper archery safety gear, such as armguards and finger tabs, should be worn to prevent injury.

Similar threads

Critical angle: find the depth of the fish looking up
Replies
4
Views
2K
Optimizing Dolphin Tracking: Calculating the Angle for Dart Gun Accuracy
Replies
3
Views
2K
Calculating Real Depth from Apparent Depth and Observation Angle
Replies
8
Views
2K
Projectile motion of arrow shot parallel to ground
Replies
14
Views
5K
Man Rows Boat: Force, Angle, Velocity Examined
Replies
15
Views
2K
What is the Recoil Velocity of a Cannon Shooting a 30 kg Shell at 500 m/s?
Replies
3
Views
2K
What Angle Should the Archer Shoot the Arrow for Optimal Accuracy?
Replies
4
Views
4K
Reflection and refraction of light
Replies
4
Views
8K
B How to shoot longer shots in basketball
Replies
20
Views
2K
How Do You Calculate the Maximum Angle of Inclination After a Collision?
Replies
10
Views
3K

Hot Threads

Recent Insights

Back
Top