Angular and linear acceleration

[celeramo]

Homework Statement

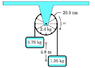
An Atwood machine is constructed using a
hoop with spokes of negligible mass. The
2.4 kg mass of the pulley is concentrated on
its rim, which is a distance 20.9 cm from the
axle. The mass on the right is 1.36 kg and on
the left is 1.79 kg.
What is the magnitude of the linear accel-
eration of the hanging masses? The accelera-
tion of gravity is 9.8 m/s^2

Answer in units of m/s^2

Homework Equations

F=ma
$$\tau$$=I $$\alpha$$
$$\alpha$$ R=v

The Attempt at a Solution

Ok I found the net force action on the system as the difference of the two weight forces so:
F1=1.79*9.8=17.542N F2=1.36*9.8=13.328N
Fnet=4.214N

Now I said that F=ma, but since the wheel has a mass, and thus a moment of inertia I said:
F=(m1+m2)a+I$$\alpha$$ where m1 and m2 are the weights and I is the moment of inertia and alpha is the angular acceleration of the wheel
I think this is probably where I am mistaken...but continuing from here

I=mr^2=2.4*(.209^2)=.104834

and I say a=$$\alpha$$r

4.214=(3.15 kg)a+I*a/r
4.214=3.15a+.501598a => 4.214=(3.6516)a
a=1.15402 m/s^2

and needless to say this is incorrect :(

Any help would be wonderful! Thanks a lot

 

[Dr.D]

You need to draw a FBD for each of the three bodies (two falling masses and the wheel) and let that guide you to writing your equations.

 

[celeramo]

Ok, I have figured it out by drawing a FBD and treating the weights as torques on the wheel. But I am still curious and would like to know at what point what I attempted becomes invalid?

 

[Dr.D]

I'll let you figure that out.