palaphys
- 266
- 17
- Homework Statement
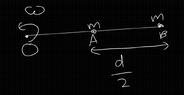
- A light rod is rotating on a frictionless horizontal table about one of its ends such that a mass is attached to its center and to its other end. What is the angular momentum of the mass at the other end with respect to the center?
- Relevant Equations
- L=Iw L=mvr
So my first approach was to use L=Iw.
Computing I, moment of inertia,I=$$I_{center} = \frac{md^2}{4}$$
$$L_{center} = I_{center} \omega = \frac{md^2\omega}{4}$$
And hence I obtain an answer.
However, when I further thought about the question, I realised that L is a vector and I can probably do this:
$$L_{ab} =L _{ao} - L_{bo} $$
Where b is the particle at the center and a is the particle at the end.
But that's when:
$$\begin{align*}
L_{B/A} &= md^2\omega - \frac{md^2\omega}{4} \\
L_{B/A} &= \frac{4md^2\omega}{4} - \frac{md^2\omega}{4} \\
L_{B/A} &= \frac{3md^2\omega}{4}
\end{align*}$$
Why are the results different?
Computing I, moment of inertia,I=$$I_{center} = \frac{md^2}{4}$$
$$L_{center} = I_{center} \omega = \frac{md^2\omega}{4}$$
And hence I obtain an answer.
However, when I further thought about the question, I realised that L is a vector and I can probably do this:
$$L_{ab} =L _{ao} - L_{bo} $$
Where b is the particle at the center and a is the particle at the end.
But that's when:
$$\begin{align*}
L_{B/A} &= md^2\omega - \frac{md^2\omega}{4} \\
L_{B/A} &= \frac{4md^2\omega}{4} - \frac{md^2\omega}{4} \\
L_{B/A} &= \frac{3md^2\omega}{4}
\end{align*}$$
Why are the results different?