mizzy
- 217
- 0
Homework Statement
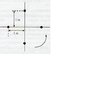
The system of point masses m shown in the above figure is rotating at an angular velocity of 2rev/s. The masses are equal and connected by light flexible spokes that can be lengthened or shortened. What is the new angular velocity if the spokes are shortened from 1m to 0.5m?
Homework Equations
The Attempt at a Solution
Not sure how to approach this question. Someone please guide me.