Angular Velocity and Acceleration of a Rotating Rod: Homework Problem

[Karol]

Homework Statement

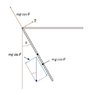
A rod of length L and mass m which is free to rotate round it's edge is held, initially, horizontally.
What are: the angular velocity and acceleration at angle θ
The force at the nail (the axis)

Homework Equations

Torque and moment of inertia: $M=I\alpha$

The Attempt at a Solution

Conservation of energy:
$$mg\frac{L}{2}\cos\theta=\frac{1}{3}mL^2\omega\;\rightarrow \omega=\frac{3}{2}gl\cos\theta$$
$$M=I\alpha:\; mg\frac{L}{2}\sin\theta=\frac{1}{3}mL^2\alpha\;\rightarrow \alpha=\frac{3g}{2L}\sin\theta$$
The linear, tangential acceleration $a_t=\alpha\frac{L}{2}$
I take forces in the tangential direction, F is the reaction:
$$mg\frac{L}{2}\sin\theta-F=m\cdot \frac{3g}{2L}\sin\theta \frac{L}{2}\;\rightarrow\; F=\frac{1}{4}mg\sin\theta$$
But i am not sure.
The reverse of the axial component of gravity $mg\cos\theta$ is the second component of the reaction in the nail.

 

[haruspex]

$mg\frac L2 \cos\theta=\frac 13mL^2\omega$

You seem to be mixing energy and angular momentum.

 

[Karol]

$$mg\frac{L}{2}\cos\theta=\frac{1}{2} \frac{1}{3}mL^2\omega^2\;\rightarrow \omega^2=\frac{3g\cos\theta}{L}$$

 

[haruspex]

$$mg\frac{L}{2}\cos\theta=\frac{1}{2} \frac{1}{3}mL^2\omega^2\;\rightarrow \omega^2=\frac{3g\cos\theta}{L}$$

Right.

 

[Karol]

But what about the main question, the force on the nail?

 

[haruspex]

But what about the main question, the force on the nail?

The force will depend on the rate of rotation (centripetal force), which you seem to have omitted.

 

[Karol]

The force will depend on the rate of rotation (centripetal force), which you seem to have omitted.

The centripetal force on the COM at the distance L/2: $m\omega^2\frac{L}{2}$ is added:
$$mg\frac{L}{2}\sin\theta-F=m\cdot \frac{3g}{2L}\sin\theta \frac{L}{2}\;\rightarrow\; F=\frac{1}{4}mg\sin\theta$$
$$F_{tot axial}=\frac{1}{4}mg\sin\theta+m\omega^2\frac{L}{2}$$

 

[haruspex]

The centripetal force on the COM at the distance L/2: $m\omega^2\frac{L}{2}$ is added:
$$mg\frac{L}{2}\sin\theta-F=m\cdot \frac{3g}{2L}\sin\theta \frac{L}{2}\;\rightarrow\; F=\frac{1}{4}mg\sin\theta$$
$$F_{tot axial}=\frac{1}{4}mg\sin\theta+m\omega^2\frac{L}{2}$$

F is the component of the axial force parallel to the motion of the mass, i.e. tangential, no?
You need to find the total radial force (including the centripetal force) and add that vectorially.

 

[Karol]

F is the component of the axial force parallel to the motion of the mass, i.e. tangential, no?

Yes, i made a mistake.
$$\left\{ \begin{array}{l} F_{tan}=\frac{1}{4}mg\sin\theta \\ F_{rad}=mg\cos\theta+m\omega^2\frac{L}{2} \end{array} \right.$$

 

[haruspex]

Yes, i made a mistake.
$$\left\{ \begin{array}{l} F_{tan}=\frac{1}{4}mg\sin\theta \\ F_{rad}=mg\cos\theta+m\omega^2\frac{L}{2} \end{array} \right.$$

That looks right.

 

[Karol]

Thanks

 

[SammyS]

Karol,

Should this title actually be "Rod rotating round it's end" ? -- not edge

 

[Karol]

Karol,

Should this title actually be "Rod rotating round it's end" ? -- not edge

Yes, correct, i don't know physics AND english well...