Ann's questions at Yahoo Answers regarding finding tangent lines

[MarkFL]

Here are the questions:

Differentiate each function and find the equation of the tangent line at x=a?

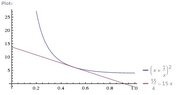
1. y=(x+(1/x))^2 ; a=0.5
I took the derivative and got 2(x+(1/x))(1-(1/(x^2))

I plugged a=0.5 for x and got y=6.25

What is y' and how do I plug this into slope-intercept form to find the equation?

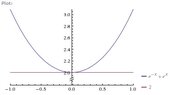
2. y=e^x+e^-x ; a=0

I took the derivative and got e^x-e^-x.

I plugged 0 in for x and got y=2

What is y' and how do I plug this into slope-intercept form to find the equation?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Ann,

1.) We are given:

\(\displaystyle f(x)=\left(x+\frac{1}{x} \right)^2=x^2+2+x^{-2}\)

Although not necessary, I have expanded the function just to make differentiation a bit easier. So, differentiating, we find:

\(\displaystyle f'(x)=2x-2x^{-3}=\frac{2\left(x^4-1 \right)}{x^3}\)

Now, the tangent line at $x=a$ can be found since we have the point $\left(a,f(a) \right)$ and we have the slope $m=f'(a)$. Applying the point-slope formula, we get the equation of the tangent line as:

\(\displaystyle y-f(a)=f'(a)(x-a)\)

Arranging in slope-intercept form, we have:

\(\displaystyle y=f'(a)x+\left(f(a)-af'(a) \right)\)

Using $f(x)$ and $f'(x)$, we have:

\(\displaystyle f(a)=a^2+2+a^{-2}\)

\(\displaystyle f'(a)=\frac{2\left(a^4-1 \right)}{a^3}\)

and so, the tangent line, in terms of the parameter $a$, is:

\(\displaystyle y=\left(\frac{2\left(a^4-1 \right)}{a^3} \right)x+\left(a^2+2+a^{-2}-\frac{2\left(a^4-1 \right)}{a^2} \right)\)

Simplifying, we obtain:

\(\displaystyle y=\frac{2\left(a^4-1 \right)}{a^3}x+\frac{\left(1+a^2 \right)\left(3-a^2 \right)}{a^2}\)

Now, plugging in \(\displaystyle a=\frac{1}{2}\), we get:

\(\displaystyle y=-15x+\frac{55}{4}\)

Here is a plot of the function and its tangent line:

View attachment 981

2.) We are given:

\(\displaystyle f(x)=e^{x}+e^{-x}\)

Differentiating, we find:

\(\displaystyle f'(x)=e^{x}-e^{-x}\)

Using the point $(a,f(a))$ and the slope $f'(a)$, we find the tangent line is:

\(\displaystyle y-f(a)=f'(a)(x-a)\)

Arranging in slope-intercept form, we have:

\(\displaystyle y=f'(a)x+\left(f(a)-af'(a) \right)\)

Using $f(x)$ and $f'(x)$, we have:

\(\displaystyle f(a)=e^{a}+e^{-a}\)

\(\displaystyle f'(x)=e^{a}-e^{-a}\)

and so, the tangent line, in terms of the parameter $a$, is:

\(\displaystyle y=\left(e^{a}-e^{-a} \right)x+\left(e^{a}+e^{-a}-a\left(e^{a}-e^{-a} \right) \right)\)

Simplifying, we obtain:

\(\displaystyle y=\left(e^{a}-e^{-a} \right)x+\left((1-a)e^{a}+(1+a)e^{-a} \right)\)

Now, plugging in \(\displaystyle a=0\), we get:

\(\displaystyle y=2\)

Here is a plot of the function and its tangent line:

View attachment 982