GregA said:
Thanks for all your replies and help...after having a bit of sleep I'm ready to try again...
The base is n = 1.. this gives us 2*2 - 1, a 3 square tile
What's important is not the number of tiles but the fact that the region can be covered will the L-shaped tiles. In the case of n=1, you have a single L-shaped space after removing any 1 suare from the 2 X 2 grid. Hence, the n=1 grid can be successfully tiled.
1) Let a 2^k x 2^k -1 board be tileable for all k
If this is true then it is tileable for k+1
The first assumption is a correct step. The statement following that assumption is a statement you are not allowed to make yet. How can you say that it is also tileable for k+1, unless you've proved it. But you have not proved it...so don't say it yet.
2) 2^{k+1} x 2^{k+1} - 1 = 4(2^{2k} - 1)
4(2^{2k} - 1) = 3(2^{2k}) + (2^{2k} - 1)
There's an error in where you're closing your parantheses. In the first line, the LHS is odd but the RHS is even. Anyway, what are you trying to show here ? Just by showing that two different shapes have the same number of tiles doesn't prove that they are the same shape - only that they have the same area.
What you want to prove here is that a 2^(k+1) X 2^(k+1) board is made up of 4 2^k X 2^k boards. This is done simply by noting that quartering a square board results in 4 square pieces, each with half the side of the original square. Nothing much more leaborate than that is required. The final bit here is to note that there must now be a missing tile in one of the 4 smaller boards.
3) Now we know that the (2^{2k} - 1) board is tileable.
Correct.
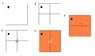
Let there be four quadrants in a 2x2 arrangement,
The 4 smaller 2^k X 2^k boards can be arranged to make the bigger board only by arranging them in a 2X2 grid. You needn't assume something that has to be true.
and that this board occupies the top right quadrant,
This statement can be made without loss of generality.
let the missing tile also be at the top right.
This assumption is illegal, and unnecessary. It is illegal because you are required to prove something no matter what the position of that tile. And it is unnecessary because it doesn't affect what you are now goingto do with the other 3 boards.
4) The three boards remaining are (2^{2k}) in size.
3(2^{2k}) = 3(2^{2k}-1) +3 so we have another 3 boards that we know are tileable, but we have 3 holes remaining.
This doesn't mean that each board has one hole missing. Further, you don't even have to do this calculation. All you need to say is : "The 3 remaining boards are complete 2^k X 2^k boards. We know (from [2]) that we can tile a 2^k X 2^k board if there is a missing square anywhere on the board. So, we tile these 3 boards in a manner that leaves the missing square at a corner. We now rotate these 3 boards till the 3 untiled squares occupy 3 of the 4 neighboring squares of the central node (or vertex, defined as the intersection of 2 lines) of the bigger board. These 3 tiles, hence, form an L-shape that can be filled by another single L-tile. The 2^(k+1) X 2^(k+1) board has now been tiled, leaving one square vacant. (ie : P(k+1) has been proven to be true if P(k) is true).
Let each each 3 boards occupy one quadrant each, and their missing tiles be positioned on its board opposite to the location of its quadrant.
This ensures that there are 3 gaps at the centre.
5) Finally due to the fact that the quadrants are in a 2x2 arrangement it folows that only 2 missing tiles at the centre can be on the same axis such that one must be above (or to the right of) the other 2...and as they all meet this fits the requirement for a 3 square L shaped tile.
As we now have 3 tileable boards, each sharing one 3 square L shaped tile and one additional board with its hole missing. we have now have a
(2^{2(k-1)} - 1) board that has been proven to have been made up of 4(2^{2k} - 1) boards with an additional L shaped tile at the centre.
This is okay too, if perhaps, a little excessively descriptive.
But you need to made a final closing statement - the point of the induction method. So far, you've only proved that the bigger board can be tiled assuming the smaller board can be tiled, so you need to finish with something like :
"Thus, by induction, it follows that any board of size 2^n X 2^n with one missing tile anywhere on it can be covered with L-shaped 3-square tiles."