naznad
- 4
- 0
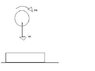
A spherical ball of radius r and mass m colides with a plank og mass M on a smooth horizontal surface.Before impact, the centre of the ball has a velocity vo( v knot) and angular velocity wo( omega knot) as I've shown in the figure.The norm velocity is reversed with same magnitude and the ball stops rotating after impact.Find the distance on the plank between the first two impacts of the ball.The coefficient of friction between the ball and the plank is µ.Assume that the plank is large enough.
I tried it out this way:
since the ball stops rotating, all of its rotational energy is imparted as translational energy to the plank in the left direction.Also frictional force will act at the point of contact in the same direction.
Therefore, rotational energy + the kinetic energy due to friction = kinetic energy of the plank.
or in terms of forces,
torque/mass m + µmg = Ma (where a is the acc. of the plank)
but i got stuck in writing the eqns.
I tried it out this way:
since the ball stops rotating, all of its rotational energy is imparted as translational energy to the plank in the left direction.Also frictional force will act at the point of contact in the same direction.
Therefore, rotational energy + the kinetic energy due to friction = kinetic energy of the plank.
or in terms of forces,
torque/mass m + µmg = Ma (where a is the acc. of the plank)
but i got stuck in writing the eqns.