Answering Questions on Graph of Toy Car Velocity

[billybobay]

1. Do my answers seem correct? I had a hard time interrupting the graph at first. The graph for the question is attached at the bottom. I would appreciate any direction or help ifthings are felt to be wrong!

Homework Statement
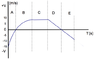
The graph above shows the velocity of a toy car being pushed by a small child along a straight line. Use the labeled sections of the graph or specific points or values to answer the following.

What is the maximum speed of the car?
Does the car ever stop? If so, where?
Where is the velocity of the car constant?
Where is the acceleration of the car constant?
Where is the total force on the car directed opposite to the car's motion?
Where is the total force on the car zero?

The Attempt at a Solution

The maximum speed of the car is approximately 8 meteres per second.
The car doesn't ever stop and travels at various velocities the entire time.
The car's velocity is constant the entire part of C.
The acceleration of the car is constant through negative acceleration or deceleration in parts D and E of the graph, it's close in part A of the graph but isn't a straight line and is slightly curved.
In parts A and E of the graph the total force on the car is directed opposite to the motion, because there's toy car is moving in the reverse direction, as shown by its negative velocity, than it through parts B through D of the graph.
The total force of the car is 0 through part C. The toy car is moving at a constant speed, and when moving at a constant speed there is no force.

 

[Simon Bridge]

The car doesn't ever stop and travels at various velocities the entire time.

... doesn't the car stop when it's velocity is zero?

The acceleration of the car is constant through negative acceleration or deceleration in parts D and E of the graph, it's close in part A of the graph but isn't a straight line and is slightly curved.

Nicely done, just a niggle - not all negative accelerations are decelerations ... the car could be increasing speed in the negative direction.

In parts A and E of the graph the total force on the car is directed opposite to the motion, because there's toy car is moving in the reverse direction, as shown by its negative velocity, than it through parts B through D of the graph.

The velocity does not have to be negative for the applied force to oppose it.
The net force is in the direction of the acceleration (Newton's second law.)

Take another look... be mindful of what the minus signs are telling you.

For instance - through D and E, the car slows down at a constant rate, comes to rest (v=0), then changes direction, picking up speed. The force opposed the motion in D and is in the same direction as the motion in E.