Apparent weightlessness problem?

[toothpaste666]

Homework Statement

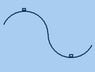
A roller coaster goes over the top of a semicircular track of radius R with a velocity Vtop, such that passengers momentarily feel weightless (zero 'g') at the top. The rollercoaster then accelerates to the bottom of another semicircular track of the same radius R. What effective 'g' do the passengers feel at the bottom? The difference in height between the top and bottom is 2R. (picture attached)

Homework Equations

F = G\frac{m1m2}{r^2}

F = ma = \frac{mv^2}{r}

E = U + K ?<br />

The Attempt at a Solution

I am kinda confused as to how to solve this problem. I am also not entirely sure what they are asking or what my answer should look like or be in terms of. It looks like one of those problems that you solve using conservation of energy where I could make y1 = 2R v1 = Vtop, y2 = 0 and v2 =??, but since they didnt give any information on friction and this type of problem wouldn't give me any info about 'g' I am going to guess I need to use the law of universal gravitation, but I don't really know how to start.

My intuition would tell me that i should use the acceleration for circular motion formula (mv^2/r) with v as vtop and set it equal to -g. Maybe then i can solve that equality for vtop and at that point wouldn't it just be a conservation of energy problem to find the velocity in terms of g at the bottom? I am lost please help :(

 

[D H]

You do not need the universal law of gravitation to solve this problem. You can ignore the tiny change in g between the top and bottom of this ride. Just use g as the acceleration due to gravity.

Energy is indeed the key to answering this question.

 

[toothpaste666]

So I also don't need mv^2/r? What do they mean by "effective g" that the passengers feel? This is the main part that is confusing me since I don't know what my answer should be in terms of .

 

[D H]

You do need mv²/r. That's going to give you v_top, which in turn will give you v_bottom, which in turn will give you the effective g felt by the passengers.

 

[SteamKing]

If the roller coaster were just sitting on the top of the track, what 'g' value would the passengers feel?

Effective 'g' is what the passengers in the roller coaster perceive. If the passengers perceive they are weightless, it means that they experience no net acceleration in the vertical direction.

 

[toothpaste666]

ok, so this is what I now have so far:

the forces on the car at the top of the first hill:

FN-mg=ma

FN=ma+mg

In order for them to experience weightlessness they must be in free fall so the net acceleration must be zero which mean that a must = -g. This means that:

-g =\frac{Vtop^2}{R}

Vtop^2 = -gR

Now using E = K + U:

\frac{1}{2}Vtop^2 + g2R = \frac{1}{2}Vbottom^2

Vbottom = (Vtop^2+2g(2R))^\frac{1}{2}

plugging in the value we got earlier for Vtop^2:
Vbottom = (4gR-gR)^\frac{1}{2}
Vbottom = (3gR)^\frac{1}{2}

How is this?

 

[D H]

You have some sign problems. To start with, if $g$ is positive, does $V_{\text{top}}^{\,2} = -gR$ make any sense?

 

[toothpaste666]

You have some sign problems. To start with, if $g$ is positive, does $V_{\text{top}}^{\,2} = -gR$ make any sense?

ahh you are right its impossible for something squared to be negative. I thought that a had to be -g though to cancel out mg. I thought FN has to equal 0 for them to feel the apparent weightlessness?

 

[toothpaste666]

also does this mean that everything else i worked out was also wrong?

 

[D H]

You did get one thing right, that $\frac 1 2 {v_{\text{bottom}}}^2 = \frac 1 2 {v_{\text{top}}}^2 + 2gR$ -- if g is a positive number.

You have to pay attention to signs in these kinds of problems.

Hint: Kinematics tells you what the net force has to be. Dynamics tells you that some of this net force comes from gravity, the rest from something else (e.g., the normal force). It's this "something else" that you feel as weight.

 

[toothpaste666]

so could I rewrite it as

mg-FN=ma

then

mg = ma + FN

FN= mg-ma

so a=g

vtop^2 = gR

plugging that in instead the answer would be

(5gR)^\frac{1}{2}

??

 

[D H]

plugging that in instead the answer would be

(5gR)^\frac{1}{2}

??

The answer to what? You didn't say what that $\sqrt{5GR}$ represents. Presumably you are writing about the velocity at the bottom. That is indeed the correct value for the velocity at the bottom of the track. Don't be sloppy! It will get you in trouble.

Note: The question you are supposed to be answering is "What effective 'g' do the passengers feel at the bottom?"

 

[toothpaste666]

ah right... so the effective 'g' would be the net acceleration at the bottom of the track? so

abottom = \frac{Vbottom^2}{r} = \frac{5gR}{R} =5g

so the effective g would be 5g?

 

[D H]

No. You are forgetting about gravity.

That is the acceleration at the bottom of the track. The "F" in F=ma is the net force. There are two forces at play here, gravitation (directed downward) and the normal force (directed upward). These combine to yield the net force. You only feel non-gravitational forces. What must the acceleration due to non-gravitational forces be if the net acceleration is 5g upward?

 

[toothpaste666]

Ok I'm sorry haha i think i got it this time. So at the bottom of the track:
FN- mg= 5gm
FN=6gm
a = 6g

so you would feel an effective 'g' of 6g?

 

[toothpaste666]

or wait a minute am i making the same sign mistake as before? If I chose acceleration for the system to be positive downward does that mean that at the bottom of the track

mg-FN=5gm

?

but then again would that also make the 5gm be negative since its pointing upward and id end up with 6g anyway?

 

[D H]

6g is the correct answer.

At the top of the track, the roller coaster must be accelerating downward at 1g in order for the sensed acceleration to be zero. At the bottom of the track, the roller coaster is accelerating upward at 5g. That means the sensed acceleration is 6g.

 

[toothpaste666]

Thank you!