Peppino
- 39
- 0
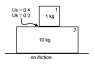
1-kg Block 1 sits on 10-kg Block 2. Friction between the blocks is 0.4 static, 0.3 kinetic while the floor is frictionless. A 4-N force is exerted on Block 1. What is the acceleration of Block 2?
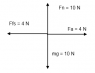
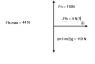
I know Block 1 won't move relative to Block 2 since it is canceled out by the frictional force, and I know Block 2 will be propelled by a frictional force. However, I am not sure which frictional forces come into play.
One way I see this is to treat both Blocks as one object, so that a 4-N force accelerates the 11-kg system at 4/11 = 0.364 m/s2. However, I'm not sure how to emulate this through each individual block in the free body diagrams.
I know Block 1 won't move relative to Block 2 since it is canceled out by the frictional force, and I know Block 2 will be propelled by a frictional force. However, I am not sure which frictional forces come into play.
One way I see this is to treat both Blocks as one object, so that a 4-N force accelerates the 11-kg system at 4/11 = 0.364 m/s2. However, I'm not sure how to emulate this through each individual block in the free body diagrams.