- #1
BlackWhole
- 2
- 0
- TL;DR Summary
- Can a black hole merger be approximated as a daughter Schwarzschild black hole created when two parent Schwarzschild black holes pack close enough together to trigger a local Schwarzschild radius containing their combined mass?
Summary: Can a black hole merger be approximated as a daughter Schwarzschild black hole created when two parent Schwarzschild black holes pack close enough together to trigger a local Schwarzschild radius containing their combined mass?
We know that the radius of the event horizon of a Schwarzschild black hole (SBH) is defined as r_s = 2*G*M/c^2, corresponding to the radius at which the escape velocity is the speed of light. For a binary black hole system, M_1 is the mass of the larger black hole and M_2 is the mass of the smaller. The LIGO event was of the merger of a 36 M_sun (where M_sun is the mass of the sun) black hole and a 29 M_sun black hole, radiating 3 M_sun equivalent energy before resulting in a 62 M_sun black hole. Thus, the larger SBH would have a Schwarzschild radius (SR) of 106 km and the smaller one would have an SR of 86 km.
If we model this super simplistically, then could we say that the black holes "merged" when they approached close enough to trigger an SBH in their vicinity? I attempted to illustrate this in the figure below.
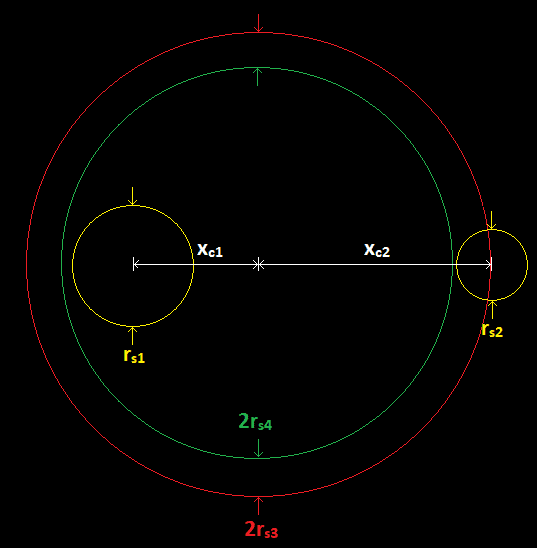
Here, r_s1 is the radius of the larger SBH, r_s2 is the radius of the smaller SBH, x_c1 is the distance from the larger SBH to the system's barycenter, and x_c2 is the distance from the smaller SBH to the system's barycenter. For a sphere centered at the barycenter with the combined system mass of 65 M_sun (the sum of the masses of the two merging SBH's), the two black holes would enter the sphere starting at x_c2 = r_s3, where r_s3 is the SR of the equivalent SBH that would exist as a replacement of the two parent black holes. Here, x_c2 = r_s3 = 192 km. Using the equation for the position of the center of mass of two point masses, we get that x_c1 = M_2/M_1*r_s3, where M_1 is the mass of the larger SBH and M_2 is the mass of the smaller SBH. Thus, the distance between the two black holes at the time of the "merge" would be d_merge = (1+M_2/M_1)*r_s3, where d_merge is the distance between them at that moment. Could we then state that the black holes "merged" when their centers were 347 km apart? We could then model the gravitational energy emission at the moment of the merger as an instantaneous decay of the merged SBH with an SR of 192 km to a "stable" SBH with an SR of 183 km. It is of course simple to note that r_s3 = r_s1+r_s2, and that d_merge > (r_s1+r_s2), meaning that the event horizons of the two merging SBH's do not touch before the merge and are in fact separated by d_separation = d_merge-r_s1-r_s2 = d_merge-r_s3 = 155 km, where d_separation is the minimum distance between the two parent event horizons.
I know that I am neglected the fact that the space occupied by the two black holes is not uniformly dense.
We know that the radius of the event horizon of a Schwarzschild black hole (SBH) is defined as r_s = 2*G*M/c^2, corresponding to the radius at which the escape velocity is the speed of light. For a binary black hole system, M_1 is the mass of the larger black hole and M_2 is the mass of the smaller. The LIGO event was of the merger of a 36 M_sun (where M_sun is the mass of the sun) black hole and a 29 M_sun black hole, radiating 3 M_sun equivalent energy before resulting in a 62 M_sun black hole. Thus, the larger SBH would have a Schwarzschild radius (SR) of 106 km and the smaller one would have an SR of 86 km.
If we model this super simplistically, then could we say that the black holes "merged" when they approached close enough to trigger an SBH in their vicinity? I attempted to illustrate this in the figure below.
Here, r_s1 is the radius of the larger SBH, r_s2 is the radius of the smaller SBH, x_c1 is the distance from the larger SBH to the system's barycenter, and x_c2 is the distance from the smaller SBH to the system's barycenter. For a sphere centered at the barycenter with the combined system mass of 65 M_sun (the sum of the masses of the two merging SBH's), the two black holes would enter the sphere starting at x_c2 = r_s3, where r_s3 is the SR of the equivalent SBH that would exist as a replacement of the two parent black holes. Here, x_c2 = r_s3 = 192 km. Using the equation for the position of the center of mass of two point masses, we get that x_c1 = M_2/M_1*r_s3, where M_1 is the mass of the larger SBH and M_2 is the mass of the smaller SBH. Thus, the distance between the two black holes at the time of the "merge" would be d_merge = (1+M_2/M_1)*r_s3, where d_merge is the distance between them at that moment. Could we then state that the black holes "merged" when their centers were 347 km apart? We could then model the gravitational energy emission at the moment of the merger as an instantaneous decay of the merged SBH with an SR of 192 km to a "stable" SBH with an SR of 183 km. It is of course simple to note that r_s3 = r_s1+r_s2, and that d_merge > (r_s1+r_s2), meaning that the event horizons of the two merging SBH's do not touch before the merge and are in fact separated by d_separation = d_merge-r_s1-r_s2 = d_merge-r_s3 = 155 km, where d_separation is the minimum distance between the two parent event horizons.
I know that I am neglected the fact that the space occupied by the two black holes is not uniformly dense.