Ebenshap
- 9
- 0
Hi,
I wanted to see if I could understand Archimedes' proof for the area of a sphere directly from one of his texts. Almost right away I was confused by the language. Archimedes lists a bunch of propositions that eventually lead up to the 25th proposition where the area of the sphere is finally explained. But I'm stuck on the 2nd proposition. I can accept that this proof is true, but I don't get why it's noteworthy.
Here's the text for the proposition:
EH/GH
becomes this:
(EH +GH)/GH which is equal to EG/GH
Why does Archimedes think this is important to establish to figure out the area of a sphere? And also what's the difference in this example between a magnitude and a line. From the language used here, they seem to be the same thing but there must be a difference. Maybe a magnitude is a line and a line is a line segment?
Thank you,
Eben
I wanted to see if I could understand Archimedes' proof for the area of a sphere directly from one of his texts. Almost right away I was confused by the language. Archimedes lists a bunch of propositions that eventually lead up to the 25th proposition where the area of the sphere is finally explained. But I'm stuck on the 2nd proposition. I can accept that this proof is true, but I don't get why it's noteworthy.
Here's the text for the proposition:
Given two unequal magnitudes, it is possible to find two unequal straight lines such that the greater straight line has to the less a ratio less than the greater magnitude has to the less.
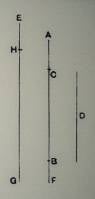
Let AB, D represent the two unequal magnitudes, AB being the greater.
Suppose BC measured along BA equal to D, and let GH be any straight line.
Then, if CA be added to itself a sufficient number of times, the sum will exceed D. Let AF be this sum, and take E on GH produced such that GH is the same multiple of HE that AF is of AC.
Thus EH/GH=AC/AF
But, since AF > D (or CB), then AC/AF<AC/CB
Therefore, componendo,
EG/GH < AB/D
Hence EG, GH are two lines satisfying the given condition.
I looked up componendo and it means to transform a fraction by adding it's denominator to it's numerator, so that this:Let AB, D represent the two unequal magnitudes, AB being the greater.
Suppose BC measured along BA equal to D, and let GH be any straight line.
Then, if CA be added to itself a sufficient number of times, the sum will exceed D. Let AF be this sum, and take E on GH produced such that GH is the same multiple of HE that AF is of AC.
Thus EH/GH=AC/AF
But, since AF > D (or CB), then AC/AF<AC/CB
Therefore, componendo,
EG/GH < AB/D
Hence EG, GH are two lines satisfying the given condition.
EH/GH
becomes this:
(EH +GH)/GH which is equal to EG/GH
Why does Archimedes think this is important to establish to figure out the area of a sphere? And also what's the difference in this example between a magnitude and a line. From the language used here, they seem to be the same thing but there must be a difference. Maybe a magnitude is a line and a line is a line segment?
Thank you,
Eben
Last edited: