- 11,326
- 8,750
A recent thread started with this OP
That OP and the answers that followed seem terribly overwrought as they struggled to answer using mostly verbage. IMO, the OP could be answered better and with less effort with a block diagram.
The OP of that quesition asked what happens if you vary one thing while holding other terms constant. That is an iappropriate question if the terms in the equation cited are related by other equations. You can't see that in a single equation, but you can see the multiple relationships in a block diagram such as below.
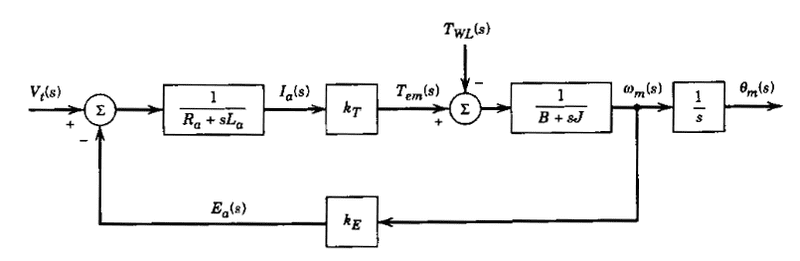
A block diagram allows one to simultaneously visualize multiple relationships, both transiently and in the steady state. For example, Q:What makes speed change? A:Torque unbalance.
You can also see in a block diagram what you can and cannot manipulate to change the steady state. (coefficients and external inputs, but not the initial value of states)
My question: Are modern engineering students expected to analyze things like motors without first learning about differential equations and Laplace transforms? If I answered a PF question with differential equations or a block diagram, would that likely be over the top and too hard to understand?
jaus tail said:I understand that from KVL
e = v -IaRa
e=k(flux)speed
speed=(constant)*(V-IaRa)/flux
But physically what causes the speed to increase?
What force causes the rotor to accelerate?
In fact physically, the rotor is moving because of field flux interacting with armature current's flux.
So physically if I reduce one flux, the speed must reduce, since i have reduced the cause of motion.
That OP and the answers that followed seem terribly overwrought as they struggled to answer using mostly verbage. IMO, the OP could be answered better and with less effort with a block diagram.
The OP of that quesition asked what happens if you vary one thing while holding other terms constant. That is an iappropriate question if the terms in the equation cited are related by other equations. You can't see that in a single equation, but you can see the multiple relationships in a block diagram such as below.
A block diagram allows one to simultaneously visualize multiple relationships, both transiently and in the steady state. For example, Q:What makes speed change? A:Torque unbalance.
You can also see in a block diagram what you can and cannot manipulate to change the steady state. (coefficients and external inputs, but not the initial value of states)
My question: Are modern engineering students expected to analyze things like motors without first learning about differential equations and Laplace transforms? If I answered a PF question with differential equations or a block diagram, would that likely be over the top and too hard to understand?