tsamocki
- 20
- 0
What if you want to rotate around something other than the x/y axis?
For example:
y=x, y=0, x=1, rotated around the line x=-1

or
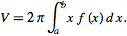
V= ⌠(between 0 and 1)π[1+x]^2 dx
= π(1/3(x)^3+x^2+2x),x=0, x=1
=π((1/3)(1)^3+(1)^2+2(1))-0
= 10π/3
Shell method:
V= ⌠(between 0 and 1)2πx(x+1)dx
=2π((1/2)x^2+(1/3)x^3)x=1,x=0
=2π((1/2)+(1/3))-0
=2π(5/6)
=5π/3
Obviously the two answers do not match (i don't even know if i am correct on either); where am i going wrong?
Thanks in advance!
For example:
Homework Statement
y=x, y=0, x=1, rotated around the line x=-1
Homework Equations
or
The Attempt at a Solution
V= ⌠(between 0 and 1)π[1+x]^2 dx
= π(1/3(x)^3+x^2+2x),x=0, x=1
=π((1/3)(1)^3+(1)^2+2(1))-0
= 10π/3
Shell method:
V= ⌠(between 0 and 1)2πx(x+1)dx
=2π((1/2)x^2+(1/3)x^3)x=1,x=0
=2π((1/2)+(1/3))-0
=2π(5/6)
=5π/3
Obviously the two answers do not match (i don't even know if i am correct on either); where am i going wrong?
Thanks in advance!