Jhenrique
- 676
- 4
I found this matrix in the wiki:
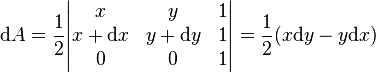
https://fr.wikipedia.org/wiki/Vites...luation_en_coordonn.C3.A9es_cart.C3.A9siennes
I think that it is very interesting because it express d²A not trivially as dxdy. So, I'd like of know if exist a matrix formulation for volume element and area element in others coordinate system...
https://fr.wikipedia.org/wiki/Vites...luation_en_coordonn.C3.A9es_cart.C3.A9siennes
I think that it is very interesting because it express d²A not trivially as dxdy. So, I'd like of know if exist a matrix formulation for volume element and area element in others coordinate system...