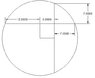
- #1
kaizokonpaku
- 7
- 0
Homework Statement
the figure is shown on the attachment. Find the area of the smallest part of the circle.
Homework Equations
area of circle, sector, segment
The Attempt at a Solution
I cannot use the said equations since the part of the circle is not with reference to the center. I cannot think also of any formulas for this kind of problem.
Please help.