Re: area using integration
If we fully factor the polynomial, we find:
$$f(x)=x^3-3x^2-x+3=x^2(x-3)-(x-3)=\left(x^2-1 \right)(x-3)=(x+1)(x-1)(x-3)$$
Hence we see the roots are:
$$x=-1,1,3$$
Because the roots are all of multiplicity 1, which simply means they are not repeated, we know the sign of $f(x)$ will alternate across the roots, so it suffices to test one interval, so let's choose $x=0$ from the interval $(-1,1)$ and we find $f(0)=3>0$.
So, we may conclude the polynomial is negative on $(-\infty,-1)$, positive on $(-1,1)$, negative on $(1,3)$ and positive on $(3,\infty)$.
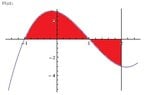
Next, let's sketch the area to be found:
View attachment 1304
Do you see now that the area under the $x$-axis will require us to integrate the negative of $f(x)$ on that interval?
When we are computing the area between two curves (and this is what we are doing if we observe that the $x$-axis is $y=0$), then we need to use as our integrand the magnitude of the difference between the two curves:
$$A=\int_a^b \left|f(x)-g(x) \right|\,dx$$
So, we need to know on what intervals $f(x)>g(x)$, since by definition:
$$|u|=u$$ when $0\le u$ and $|u|=-u$ when $u<0$.
So, we see that on $(-1,1)$ we have $0<f(x)$ and on $(1,2)$ we have $f(x)<0$, hence the area can be found with:
$$A=\int_{-1}^2\left|f(x)-0 \right|\,dx=\int_{-1}^2\left|f(x) \right|\,dx=\int_{-1}^1 f(x)\,dx+\int_1^2 -f(x)\,dx=\int_{-1}^1 f(x)\,dx-\int_1^2 f(x)\,dx$$