agnibho
- 46
- 0
Homework Statement
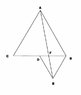
ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that :-
(i) ar(BDE) = 1/4 ar(ABC)
(ii) ar(BDE) = 1/2 ar(BAE)
(iii) ar(ABC) = 2ar(BEC)
(iv) ar(BFE) = ar(AFD)
(v) ar(BFE) = 2ar(FED)
(vi) ar(FED) = 1/2ar(AFC)
Homework Equations
The Attempt at a Solution
There was this hint :- [join EC and AD and then showing BE ll AC and DE ll AB,etc.]