Article on texture generation - can't get the math

[Artlav]

There is an article on procedural texture generation by example.
I'm trying to implement it, and got lost in the mathematics.
http://graphics.cs.kuleuven.be/publications/LVLD10PISTE/

The outline of the algorithm is thus:
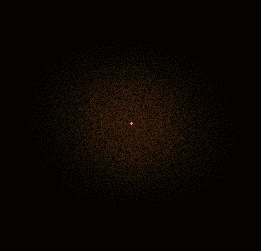
We start with a noise-like photo.

Do a 2D DFT of it:

Compute the power band coefficients and reconstruct the image with wavelet noise:

Wavelet noise is band limited, which makes it a good base block for such synthesis:

That's the theory.

In practice, i can't figure out the formula for the coefficients.

Formula (E is the input image):

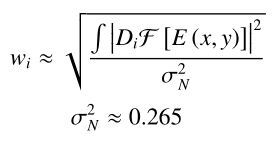
Definition of the power band:

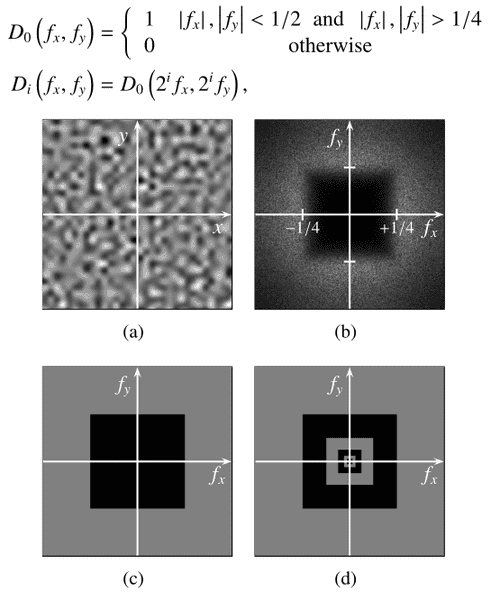
What does it mean?
Should i sum all the magnitudes of the elements in each band?
This gives me nonsense if i divide it by the amount of elements, and randomly unscaled value if i don't (that's the above picture, guesstimately scaled).
If i sum the real parts of the elements, then i get wildly wrong and out of scale figures. Normalising them also gives me something plausible.
And so on, for any way i can think of.

I guess i misunderstand something in the notation.
Does the integral sign means summing here?
Or how should i read it?

That's basically the question - what does it mean?
Bonus question - anyone heard of this method being used somewhere? A working implementation to peek at would be nice.

 

[jvicens]

Hello there,

Thank you for bringing this topic to our attention. I am familiar with the concept of procedural texture generation and have also come across this particular article before. Let me try to help you understand the formula and how to approach implementing it.

First, let's break down the formula and understand each component:

1. E is the input image, which in this case is the noise-like photo.
2. The integral sign does indeed mean summing here. In this case, we are summing over all the pixels in the image.
3. The function F is the Fourier transform of the input image E.
4. The function W is a filter function, which is used to limit the frequencies in the image. This is what gives the wavelet noise its characteristic band-limited nature.
5. The function G is the inverse Fourier transform of the filtered image, which gives us the final reconstructed image.

Now, to answer your question about the power band coefficients, they represent the magnitude of the Fourier coefficients at different frequency bands. In simpler terms, they tell us how much of each frequency is present in the image.

To calculate these coefficients, you will need to follow these steps:

1. Take the Fourier transform of the input image E.
2. Multiply the resulting Fourier coefficients with the filter function W.
3. Take the inverse Fourier transform of the filtered coefficients.
4. Calculate the magnitude of the resulting coefficients.
5. Sum the magnitudes of the coefficients in each frequency band, as defined by the filter function W.

To answer your bonus question, yes, this method has been used in various applications such as texture synthesis, image manipulation, and even in computer graphics for creating realistic textures. As for a working implementation, I suggest searching online for sample code or reaching out to the authors of the article for assistance.

I hope this helps in your understanding and implementation of the algorithm. Good luck!