romogirl
- 4
- 0
Homework Statement
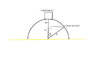
An ice cube is placed on top of an overturned spherical bowl of radius r, as indicated in the figure. If the ice cube slides downward from rest at the top of the bowl, at what angle θdoes it separate from the bowl? In other words, at what angle does the normal force between the ice cube and the bowl go to zero?
Homework Equations
∑F=ma
ΔK=-ΔU
The Attempt at a Solution
I drew a free body diagram, with the force on the ice cube from the Earth pointed straight down and the normal force perpendicular to the surface of the globe. I then summed the forces.
ΣFy=Wy-N=mac
Based on trig, I know that Wy= cosθW = cosθmg.
Then: ac= Vt2/r and the normal force is 0. Substituting all this in I get:
cosθmg=mVt2/r
cosθ=Vt2/gr
So the next step would be to find for Vt.
ΔK =-ΔU
Kf =1/2mv2
KO = 0
Uf = 0
UO = mgr
1/2mv2 = mgr
v2 = 2gr
Plugging in this to the above:
cosθ=2gr/gr
cosθ=2
which isn't the answer.
I think I am making a mistake possibly in Uf, but I am not sure what exactly it would be. Would it be mgh, where h is the height it falls off? How would I find h then?