Balancing a Plank on a Cylinder: Investigating Potential Energy Gain

[theloathedone]

Homework Statement

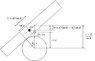
A uniform plank of thickness 2d and weight W is balanced horizontally across the top of a circular cylinder of radius r, whose axis is horizontal and perpendicular to the length of the plank. Prove that the gain of potential energy when the plank is turned without slipping through an angle theta in a vertical plane is:
$W(r \sin{\theta} -(r+d)(1-\cos{\theta}))$

Homework Equations

Clearly this is a problem of gravitational potential energy, U = mgh.

The Attempt at a Solution

I drew the diagrams, which are attached.
So from diagram 2, I get
$\inc U=W(\frac{r+d}{\sin{\theta}}-(r+d)-((r+d)\tan{\theta}-r\theta)\sin{\theta}))$
which is completely unlike what is to be proved.
I'm at a dead end and not sure how to proceed, thanks in advance for the help!

 

[verty]

I think the length $$\frac{r+d}{sin\theta}$$ is incorrect. If you fix that, you should be able to simplify the formula considerably.

I would also suggest trying to find an easier formula by adding two lengths.

 

[theloathedone]

Hmm ok I see that it should have been $\frac{r+d}{\cos{\theta}}$ instead.

But I'm not sure how to find the two lengths to add to get the correct answer still.