Ball rolling down an incline between 2 rails

[Eigenvector]

The problem is modeling a solid ball or radius R rolling down an incline of angle Theta. Note that I am an Electrical Engineer who is somewhat flaky with rotational concepts (but not completely useless :p). If the ball was rolling down a road (or any solid, flat surface), I get the following equations (which I believe neglect friction EXCEPT for causing the ball to roll):

F_x = mg sin (Theta)

T = I * (d^2x/dt^2)/R

Which, after subbing in for I (2/5*mR^2) and converting to linear displacement by multiplying by R, I get a rotational displacement force of F_rx = 2/5m (d^2x/dt^2).

Combining these two equations, we get:

m(d^2x/dt^2) = mg sin (Theta) - 2/5m(d^2x/dt^2). which can be rearranged as

(d^2x/dt^2) = 5/7gsin(Theta).

We then linearize about small Theta, and get a transfer function between position and Theta of (5/7g)/s^2.

Now, I have two questions:

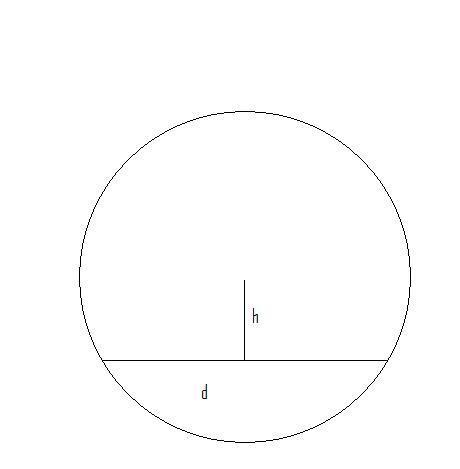
#1 If instead of a solid surface, we instead (and this is the actual experimental setup) we have a ball placed between 2 rails a distance d apart. Do I need to find the "effective radius of the ball", i.e., h from the following diagram and use that to calculate both the displacement of the ball (so converting the Torque equation to position), and through use of the // axis Theorem for finding I?

#2 When comparing experimental to simulated data with the above model, no "gain value" for the transfer function fits the data (i.e, the curve has a fundamentally different shape than what our model predicts). I thought that this was due to un-modeled friction effects. Is that correct or is this the result of something else?

 

[rcgldr]

Both the torque and the rolling speed would be relative to the effective radius. The track width would have to be very precise, not vary with position, and not expand due to the balls weight in order for the effective radius to not have a dynamic effect. Fiction could be an issue with a softer ball, since the rails "squeeze" the ball. Steel on steel might work if the ball doesn't slide. Aerodynamic drag and normal rolling resistance is another issue.

 

[Emreth]

You're missing a term for the translation inertia of the sphere.Also T is wrong, it has to be angular acceleration. There's an easier way to do this analysis using total energy.Say initial position is at a height z0=0 so that deltaz is z. (z is vertical direction, deltaz=z-z0). At any z value, the energy balance is mgz=1/2mv^2+1/2Iw^2 (v is the velocity in z direction, w is the angular speed). Now there's a geometric relationship between v and w if we assume there's no sliding. v=w*R*sin(teta). (you can calculate it like this, if the ball rolls down some angle in radians teta2, it goes (teta2/2pi)*2*pi*R*sin(teta) distance in the z direction.) I is 2/5mR^2. So you put everything together and solve v in terms of z.
I think it becomes v=sqrt(gz/(0.5+0.2(sinteta)^2)). if you're trying to find velocity in the xprime direction-on the wedge, z=xprime*sinteta. you can recollect terms to get this
v=sqrt(10*g*xprime*(sinteta)^3/(5*(sinteta)^2+2)) .Use xprime/t=v.Then you can find xprime and/or v as a function of t and teta.
As long as you don't have sliding on the rails, it doesn't matter if you have a solid block or rails.