- #1
Andy Froncioni
- 2
- 1
(This is NOT a homework problem. It's an engineering problem I'm trying to crack.)
A wheel with a rubber tire (friction) can roll on a suspended rail. Attached to it is a pendulum that's rigidly mounted on the axle of the wheel with a mass that can hand down and swing. (The wheel's rotation and the pendulum's are coupled.)
The system swings freely and due to the energy lost to rolling resistance of the tire against the rail ( F = N*Crr ), the system's amplitude decreases over time.
I am trying to find the dynamical equations of motion of this system.
d (theta)/dt = alpha
d(alpha)/dt = f(Crr,M,L,R,m,...)Can anyone help me? I know the equation for the normal force on the wheel axle is given by something like:
N - M*g - m*v^2/L cos(theta) = 0, where
N = normal force
M is the total mass of the system
m is the effective mass of the pendulum portion
v is the velodity of the COM of the pendulum portion
theta is the angle of the pendulum to the vertical
Crr is the coeff of rolling resistance of the tire
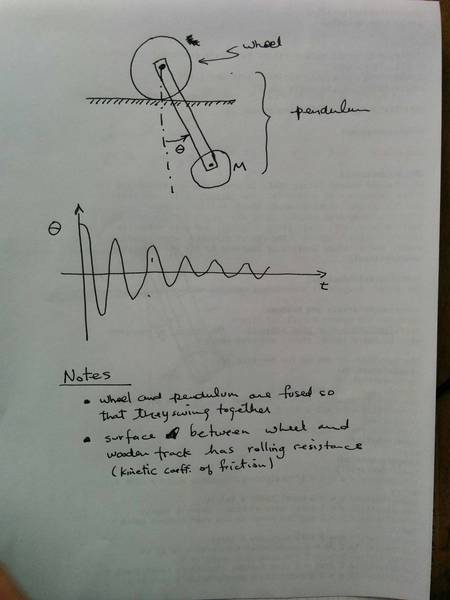
A wheel with a rubber tire (friction) can roll on a suspended rail. Attached to it is a pendulum that's rigidly mounted on the axle of the wheel with a mass that can hand down and swing. (The wheel's rotation and the pendulum's are coupled.)
The system swings freely and due to the energy lost to rolling resistance of the tire against the rail ( F = N*Crr ), the system's amplitude decreases over time.
I am trying to find the dynamical equations of motion of this system.
d (theta)/dt = alpha
d(alpha)/dt = f(Crr,M,L,R,m,...)Can anyone help me? I know the equation for the normal force on the wheel axle is given by something like:
N - M*g - m*v^2/L cos(theta) = 0, where
N = normal force
M is the total mass of the system
m is the effective mass of the pendulum portion
v is the velodity of the COM of the pendulum portion
theta is the angle of the pendulum to the vertical
Crr is the coeff of rolling resistance of the tire