Ball Rotation on a Ball: Solving for Center of Mass Velocity

[Karol]

Homework Statement

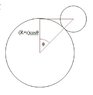
A ball of mass m and radius r starts off on top of a fixed ball of radius R. it rotates down without slipping.
What's the ball's center of mass velocity as a function of θ.
The angular velocity is ω.

Homework Equations

Moment of inertia: $I=\frac{2}{5}mr^2$
Potential energy: $E_p=mgh$
Kinetic energy due to rotation: $E_ω=\frac{1}{2}I\dot\theta^2$

The Attempt at a Solution

Kinematics: the path the small ball makes is equal to the path on the big one, and so are the angular velocities
$$R\dot\theta=r\omega\rightarrow\omega=\frac{r}{R}\dot\theta$$
The height of the ball's center during the fall is $(R+r)\cos\theta$
Total energy at the top, relative to the center, is equal during the fall:
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\omega^2+mg(R+r)\cos\theta$$
$$mg(R+r)=\frac{mr^2}{5}\frac{R^2}{r^2}\dot\theta^2+mg(R+r)\cos\theta$$
The center of the ball's velocity is $v=(R+r)\dot\theta$
I can't solve for v, and the answer should be an isolated v

 

[RyanH42]

whats the meaning of isolated v ? If you can give me an example I can solve the question.

 

[theodoros.mihos]

I think $v$ is $v_{cm}$. Check your 1st equation for energy consevation. Is it correct?

 

[Karol]

Check your 1st equation for energy consevation. Is it correct?

$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\omega^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
kinematics:
$$v_{cm}=(R+r)\dot\theta\rightarrow\dot\theta^2=\frac{v_{cm}^2}{(R+r)^2}$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\frac{R^2}{r^2}\dot\theta^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\frac{v_{cm}^2}{(R+r)^2}+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$v_{cm}^2=\frac{10g(R+r)^3(1-\cos\theta)}{2R^2+5(R+r)}^2$$
It's not right

 

[theodoros.mihos]

$\omega$ is not $\dot{\theta}$. The ratio is $\frac{\omega}{\dot{\theta}} = \frac{R}{r}$

 

[RyanH42]

If you know th exact answer can you tell me ? I solved it I guess.I think your equation is wrong why there is $(R+r)mg$ and the other side $(R+r)mgcosθ$

 

[Karol]

$\omega$ is not $\dot{\theta}$. The ratio is $\frac{\omega}{\dot{\theta}} = \frac{R}{r}$

But i have done that in:
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\omega^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\frac{R^2}{r^2}\dot\theta^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$

 

[theodoros.mihos]

Ok. You are make correct inside equation.

 

[RyanH42]

Why there's two potantial energy ? Can somebody give me an answer ??

 

[theodoros.mihos]

The right hand is the potential energy to arbitrary angle $\theta>0$.

Your answer is correct. The angle that the small ball leave the big ball surface is another question.

 

[RyanH42]

In yor perspective the potantial energy on "top" will be zero that's nonsense.The total potantial energy is $mg(R+r)(1-cosθ)$ or $mg(R+r)(cosθ)$

 

[theodoros.mihos]

There is a problem with the unlucky point on the attached graph. With big ball centre as origin the potential energy is $mg(R+r)\cos{\theta}$.

 

[RyanH42]

If you consider left picture you need to realize the potantial energy is cannot be zero top but If you consider right picture you will consider that potantial energy iz zero.I am not wrong which one x and which one is x-axis and which one is y-axis ? I assumed left picture and If you assumed same thing then my equation is true.But If yıu assume right pic your equation is true.

 

[theodoros.mihos]

On the OP, the potential energy variation makes the move, indepented from origin. See a better image.

 

[ChrisVer]

In your solution for v^2 why did you square the 1-\cos \theta?
Was that a typo?
Also a square should be missing from the denominator (where you add m^2 with m)

 

[ChrisVer]

Also there is no problem with the potential energy as written.
At first when the ball is on top you may say that you have potential energy mg (R+r).
Then the potential energy once the ball has taken some kinetic energies by slidding, the potential energy is mg (R+r) \cos \theta.
The zero is taken at the height of the big ball's center.

It doesn't matter where you take the zero in fact, since the potential energy of the system will have to be mg(R+r) at the beginning (at the end potential energy is not taken at a point but as the difference between two points). Either you take point A to be 0 and point B to be U, you can as well take point B to be 0 and point A will be U.

 

[ChrisVer]

*deleted found the answer*

 

[haruspex]

the angular velocities $R\dot\theta=r\omega$

Not sure if this has been pointed out already, but that is not right. E.g. consider the case where r=R and it has rolled all the way from top to bottom. $\theta = \pi$. Through what angle has the moving ball rotated?

[Edit: there is quite a quick way. Pretend that at angle $\theta$ the moving ball encounters a ramp going down tangentially to the fixed ball. Will transition to the ramp immediately change the linear or angular velocities? What is its KE now?]

 

[RyanH42]

Also there is no problem with the potential energy as written.
At first when the ball is on top you may say that you have potential energy mg (R+r).
Then the potential energy once the ball has taken some kinetic energies by slidding, the potential energy is mg (R+r) \cos \theta.
The zero is taken at the height of the big ball's center.

It doesn't matter where you take the zero in fact, since the potential energy of the system will have to be mg(R+r) at the beginning (at the end potential energy is not taken at a point but as the difference between two points). Either you take point A to be 0 and point B to be U, you can as well take point B to be 0 and point A will be U.

Thank you

 

[ehild]

The Attempt at a Solution

Kinematics: the path the small ball makes is equal to the path on the big one, and so are the angular velocities
$$R\dot\theta=r\omega\rightarrow\omega=\frac{r}{R}\dot\theta$$

As Haruspex pointed out, it is not right.
See figure.

The contact point with the sphere is the red dot on the ball. The ball rolls a distance s on the ball , so the point A moves into A', and the length of arc P1A' on the sphere is s. The angle <P'O'A' = s/r, but the ball turned by the angle <P'O'P more. The angle of turn of the ball is Φ=s/r+θ. s=θR, so Φ=(R/r+1)θ. ω=dΦ/dt and $V_{CM}=(R+r)\dot \theta$.

 

[Karol]

The contact point with the sphere is the red dot on the ball. The ball rolls a distance s on the ball , so the point A moves into A', and the length of arc P1A' on the sphere is s. The angle <P'O'A' = s/r, but the ball turned by the angle <P'O'P more. The angle of turn of the ball is Φ=s/r+θ. s=θR, so Φ=(R/r+1)θ. ω=dΦ/dt and $V_{CM}=(R+r)\dot \theta$.

I understand but can't imagine. the ball rotates only a distance s, so how can it rotate more?

 

[haruspex]

I understand but can't imagine. the ball rotates only a distance s, so how can it rotate more?

Try expressing the linear movement of the mass centre in two ways:
1. In terms of $\dot \theta$
2. In terms of $\omega$

 

[ehild]

I understand but can't imagine. the ball rotates only a distance s, so how can it rotate more?

I meant "if it rolls a distance s" along the surface of the big sphere. It can roll shorter or longer .

Draw a big circle of radius R and cut out from paper a small one with radius r=R/3, for example. Roll the small circle along the circumference of the big one and see at what angle it turns while it rolls along an arc of length equal to its own circumference, 2πr.

 

[Karol]

Theodoros and ehild, with which software did you make those sketches?

 

[Karol]

The angle the ball rotates is Φ.
$$\phi=\frac{s}{r}+\theta=\frac{R\theta}{r}+\theta=\left( \frac{R}{r}+1 \right)\rightarrow \omega=\dot\theta\left( \frac{R}{r}+1 \right)$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\omega^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\dot\theta^2\left( \frac{R}{r}+1 \right)^2+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$v_{cm}=(R+r)\dot\theta$$
$$mg(R+r)=\frac{1}{2}\left( \frac{2}{5}mr^2 \right)\frac{v_{cm}^2}{r^2}+mg(R+r)\cos\theta+\frac{1}{2}mv_{cm}^2$$
$$\rightarrow v_{cm}^2=\frac{10}{7}g(R+r)(1-\cos\theta)$$
This is indeed one of the 5 possible answers given in the test

 

[haruspex]

$\rightarrow v_{cm}^2=\frac{10}{7}g(R+r)(1-\cos\theta)$
This is indeed one of the 5 possible answers given in the test

Can you now see how to get there in a few lines using my hint in post #18?

 

[ehild]

$$\rightarrow v_{cm}^2=\frac{10}{7}g(R+r)(1-\cos\theta)$$
This is indeed one of the 5 possible answers given in the test

Well done!

 

[ehild]

Theodoros and ehild, with which software did you make those sketches?

Do you mean the drawing? It is Paint of Windows. https://en.wikipedia.org/wiki/Paint_(software)

 

[Karol]

[Edit: there is quite a quick way. Pretend that at angle $\theta$ the moving ball encounters a ramp going down tangentially to the fixed ball. Will transition to the ramp immediately change the linear or angular velocities? What is its KE now?]

Did you say that because i asked about the kinematic relation, in which i had a mistake, between θ and Φ(the angle the ball rotates), or do you mean that in this way i can get to the final result:
$$v_{cm}^2=\frac{10}{7}g(R+r)(1-\cos\theta)$$
Indeed i was asked about the relation v_cm and θ, so what does it help to put a ramp at θ, after the ball has already reached there?
Edit: i will try to find the velocity by considering a ball rotating down the ramp:
The tangential force applies the torque:
$$mgr\cdot\sin\theta=\frac{2}{5}mr^2\cdot\dot\omega$$
The acceleration of the COM:
$$r\dot\omega=a_{cm}$$
It doesn't help

 

[Wily Willy]

Karol,

I believe that the short cut that haruspex referred to had to do with the relationship between the little ball's angular velocity and the velocity of the center of mass. Applying this relationship early would allow you to skip a couple steps in your solution. Hope this helps.

Also, could someone explicitly state what is meant by theta with a dot on top? I don't recall this notation.

 

[Nathanael]

Also, could someone explicitly state what is meant by theta with a dot on top? I don't recall this notation.

\dot \theta is shorthand notation for the time derivative of θ (that is, \dot \theta \equiv \frac{d\theta}{dt})

More generally \dot x is defined to mean \frac{dx}{dt} where x can mean pretty much anything, but t exclusively means time. (In other words, dy/dx would not be written as \dot y unless x represents time.) I think this notation is used primarily in physics, but it is used quite a bit.

Furthermore, \ddot x\equiv \frac{d^2\theta}{dt^2}

 

[Karol]

Nathanel already answerd, i erased mine

 

[Nathanael]

Karol, you can save time/effort by using the "constraint of rolling" which is v_{cm}=R\dot \phi. That solves the problem without needing to consider \dot \theta

I think Haruspex (when talking about tangent ramps) was just trying to show you that this equation is just as true on a sphere as it is on a flat surface.
(The ball rolls dΦ, it's center of mass must move a distance RdΦ, and everything is flat in this differential limit, thus v_{cm}=R\dot \phi)

 

[haruspex]

Karol, you can save time/effort by using the "constraint of rolling" which is v_{cm}=R\dot \phi. That solves the problem without needing to consider \dot \theta

I think Haruspex (when talking about tangent ramps) was just trying to show you that this equation is just as true on a sphere as it is on a flat surface.
(The ball rolls dΦ, it's center of mass must move a distance RdΦ, and everything is flat in this differential limit, thus v_{cm}=R\dot \phi)

Not exactly.
The ball's mass centre is moving at $(R+r)\dot \theta$, and it is rolling on a stationary surface, so its rotation rate is $(R+r)\dot \theta/r$. From that you can write down the KE straight away. I mentioned a ramp because I thought it make that viewpoint more apparent.

 

[Karol]

Thanks all