1MileCrash
- 1,338
- 41
Homework Statement
At what angle should the roadway on a curve with a 50m radius be banked to allow cars to make the curve at 12 m/s even if friction is 0?
Homework Equations
The Attempt at a Solution
All of the centripetal acceleration comes from normal force from the road on the car.
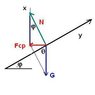
I choose to represent the road as being along the y-axis and Fn as being along +x axis. Then gravity is directed at angle theta to the left of the -yaxis.
Normal force must equal the component of gravity along -xaxis, which is mgsin(theta),
Since the required centripetal force is mv^2/r, this is 2.88m, mgsin(theta) = 2.88m
gsin(theta) = 2.88
theta = 17.09
My professors work seems to be similar, but at the end she says that:
gtan(theta) = 2.88
theta = 16.37
why?