Dan123
- 8
- 0
Homework Statement
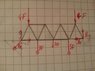
The pictue shows a symmetrical framework. I should calculate the bar forces. and make a "Clear Cut".I*m not shure because of the left movable bearing (on the left side)!?
Homework Equations
total x=0
total y=0
total M=0
The Attempt at a Solution
Here is my "Clear Cut" is it correctly?