Basic probability, conditional probability

[late347]

Homework Statement

what is the probability that a component which is still working after 800 hrs, will last for at least 900hrs

Homework Equations

conditional probability
P(E|A) = ( P( E ∩ A) ) / ( P(A) )

The Attempt at a Solution

Im just checking my own understanding if this problem is conditional probability or not.
I alraedy asked my teacher about the correct answer and I apparently had the correct answer.
But I was asked by my classmates to explain the answer, and I wasnt sure how deeply I understood the problem.

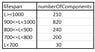
Looking at the table provided, we can see component lifetimes.

To my mind the problem can be translated into conditional probability terms such as:
"given that the component has lifetime from 800 upwards, what is probability that the component has lifetime from 900 upwards"

E : survive900hrsOrMore: (210+820) /1500 ==0,686666
A : survive800hrsOrMore: (210+820+240) /1500 == 0,846666

P(E|A) = P(E∩A) / P(A)

P(A) was calculated to be 0,846666

I think the probability of the intersection happening can be seen from the intersection in the following picture.

P(E∩A) was to my understanding calculated thusly:
(820+210)/1500 =0,686666
FavorableCases/ totalSampleSpace
in this case FavorableCases = 1030 parts that are inside the intersection
I don't know if this intersection probability can be calculated with a formula, but that seems to be how to calculate the probability of the intersection happening.

thus answer is
0,686666/ 0,846666= 0,811023

 

[Charles Link]

The way I would compute such a thing is to calculate a mean lifetime, if that is possible, and assume failures occur completely randomly and are not due to age. You can then write the probability that it will fail over a 100 hour period, basically as one minus an exponential of expected survival. $\\$ The alternative is to assume some quality factor and lower failure rate from the mean, because if it has survived for so long, it is one of those that simply doesn't fail. $\\$ This problem does appear to be somewhat subjective in the approach that is taken.

 

[Orodruin]

Looks fine to me.

 

[Orodruin]

The way I would compute such a thing is to calculate a mean lifetime, if that is possible, and assume failures occur completely randomly and are not due to age. You can then write the probability that it will fail over a 100 hour period, basically as one minus an exponential of expected survival. $\\$ The alternative is to assume some quality factor and lower failure rate from the mean, because if it has survived for so long, it is one of those that simply doesn't fail. $\\$ This problem does appear to be somewhat subjective in the approach that is taken.

I would strongly advice against this. You have a table with the appropriate observational information.

 

[late347]

Looks fine to me.

Is the intersection probability such as P(E ∩A) correctly calculated? I was googling about that thing and I just became more confused by the fomrula I found. Something like "the general multiplication rule of probability"

The examples that we had in class were mostly about simple things like:
roll one die
event A: result is odd
event B: result is >=4
find P(A∩B)
in the intersection in the die case there is only 5.
Hence 1/6 is the probability

 

[Charles Link]

Is the intersection probability such as P(E ∩A) correctly calculated? I was googling about that thing and I just became more confused by the fomrula I found. Something like "the general multiplication rule of probability"

The examples that we had in class were mostly about simple things like:
roll one die
event A: result is odd
event B: result is >=4
find P(A∩B)
in the intersection in the die case there is only 5.
Hence 1/6 is the probability

Initially I read the problem much too quickly. @Orodruin is correct. Alternatively you could simply have computed $p= 1030/1270$ and gotten the same answer. (The denominator of 1500 is present in both computations).

 

[PeroK]

thus answer is
0,686666/ 0,846666= 0,811023

Yes, it all looks good. Just a couple of points that may or may not be interesting. The number of components that fail before 800 hours is irrelevant. Another way to look at it is that you have a reduced sample space. You know you are dealing with a component that lasts 800 hours or more, so your sample space has been reduced to those 1270 components. From that point of view you can do the calculation as a direct probability of 1030/1270.

(Which I see is what @Charles Link has just said.)