- #1
stunner5000pt
- 1,461
- 2
- Homework Statement
- There are three urn contains coins
Urn 1: 5 gold coins
Urn 2: 3 gold, 3 silver
Urn 3: 3 silver
An urn is selected at randonm & a coin is drawn from the urn. If the selected coin is silver, what is the probability that urn III was selected
Determine the probability using Bayes formula & a tree
- Relevant Equations
- Bayes Formula
From my understanding of Bayes formula, it should look like something like this
[tex] P(Silver| III) = \frac{P(III | silver) \times P(silver)}{P(III)} [/tex]
now we know that P(urn III) = 1/3
and the probability of P(silver) = Pr(silver|urn I) + P(silver|urn II) + P(silver|urn III) = 1/3 (0) + 1/3 (1/2) + 1/3 (1) = 1/2
But how do i calculate P(urn 3|silver) ? Would it simply be 1/3?
If I used this, then
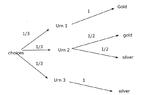
P(Silver| III) = (1/3)(1/2) / (1/3) = 1/2. is this correct?Using the tree, I have attached what I believe is the right tree.
Would the answer then be P(silver| urn III) = 1/3 / (1/2) = 2/3 ?
[tex] P(Silver| III) = \frac{P(III | silver) \times P(silver)}{P(III)} [/tex]
now we know that P(urn III) = 1/3
and the probability of P(silver) = Pr(silver|urn I) + P(silver|urn II) + P(silver|urn III) = 1/3 (0) + 1/3 (1/2) + 1/3 (1) = 1/2
But how do i calculate P(urn 3|silver) ? Would it simply be 1/3?
If I used this, then
P(Silver| III) = (1/3)(1/2) / (1/3) = 1/2. is this correct?Using the tree, I have attached what I believe is the right tree.
Would the answer then be P(silver| urn III) = 1/3 / (1/2) = 2/3 ?