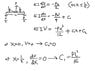Beam deflection boundary condition calculation

AI Thread Summary
The discussion centers on calculating beam deflection at specific points, L/4 and L/2, and understanding boundary conditions. The user has derived a solution for deflection but is confused about the boundary condition at x=L/2, specifically why the slope (dv/dx) is zero at this point. It is clarified that dv/dx represents the slope of the beam, and at the midpoint where the load is applied, the slope is indeed zero because the beam reaches a maximum deflection there. The user questions the physical meaning of this condition, believing that the presence of the load should prevent the slope from being zero. The conversation emphasizes the relationship between deflection, slope, and the effects of applied loads on beam behavior.
xzibition8612
Messages
137
Reaction score
0

Homework Statement



Find the deflection at x=L/4 and x=L/2 for the beam

Homework Equations



See attached pic.

The Attempt at a Solution



So I have the solution derived in class. Only 0<x<L/2 is derived because since the load on the beam is at L/2, the equation is valid for the entire beam since its symmetric (or something like that, if this isn't the correct explanation somebody tell me). My question concerns the boundary conditions. I know that at x=0, the displacement v=0. Hence you get C2=0. Now the second thing:

dv/dx=0 at x=L/2

I have no idea what dv/dx means, why its 0, and why its taken at x=L/2. Any help would be appreciated thanks.
 

Attachments

  • paint.jpg
    paint.jpg
    25.3 KB · Views: 610
Physics news on Phys.org
You ever heard of the 'slope' of the beam being discussed in your class? The slope = dv/dx.
 
ok, so what is the slope physically mean? Why is it 0 at x=L/2? It has something to do with the load P? I see that the derivative of moment is shear force, and the derivative of shear force is distributed force. But that has nothing to do with deflection right?
 
Start with deflection. What's the first derivative of a curve represent?
 
the slope, y/x. Why would dv/dx=0 at x=L/2? That makes no physical sense, because at x=L/2 there is a load P upward and it must deflect. Hence dv/dx can't be 0.
 
Last edited:
What's the slope of a curve in calculus class?
 

Similar threads

Deflection of partially loaded cantilever beam with non-homogeneous EI
Replies
3
Views
2K
Engineering Deflection and Slope of a Simply Supported Beam
Replies
8
Views
2K
Engineering Multi-point Boundary Value Problems Using Finite Difference Method
Replies
3
Views
2K
Beam Deflection: Solving with EI w''''(x) = q and Boundary Conditions
Replies
1
Views
2K
Boundary Condition for deflection of Beam
Replies
1
Views
2K
Engineering Concrete Slab Deflection Using Partial Differential Equations
Replies
11
Views
2K
Engineering How to Find the First Buckling Load from the Deflection Equation?
Replies
3
Views
2K
Solve Castigiliano Method for Continuous Beam Problem
Replies
8
Views
2K
Calculating Beam Deflection using Double Integration
Replies
10
Views
4K
Solving Beam Deflection with Singularity Equations
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top