confused_man
- 15
- 1
I'm having trouble understanding the phase shift produced by a beam splitter. I seem to be finding conflicting information.
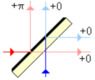
I'm specifically looking to understand a 50/50 beam splitter where one side has a dielectric mirror, as shown in this figure from wikipedia:
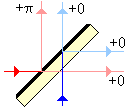
I understand the pi phase shift (due to air/dielectric reflection, where n_air < n_dielectric). Why doesn't the thickness of the beam splitter have any effect? Shouldn't there be an additional phase?
On a related note, I'm trying to see how such a beam splitter would be able to act like a Hadamard gate in quantum information, if the additional phase shift due to the thickness of the plate is included. I've seen many articles/documents say that a beam splitter can implement a Hadamard gate, but this only seems to work if the thickness of the splitter is ignored. What am I missing?
Thank you for any insight.
I'm specifically looking to understand a 50/50 beam splitter where one side has a dielectric mirror, as shown in this figure from wikipedia:
I understand the pi phase shift (due to air/dielectric reflection, where n_air < n_dielectric). Why doesn't the thickness of the beam splitter have any effect? Shouldn't there be an additional phase?
On a related note, I'm trying to see how such a beam splitter would be able to act like a Hadamard gate in quantum information, if the additional phase shift due to the thickness of the plate is included. I've seen many articles/documents say that a beam splitter can implement a Hadamard gate, but this only seems to work if the thickness of the splitter is ignored. What am I missing?
Thank you for any insight.