DeereAdam
- 9
- 0
I need to calculate how much tension it would require to bend large insulated cable of various sizes around a pulley. The Conductor would be made of aluminum or copper and solid. The Insulation would be of various thicknesses depending on the cable. I was looking at breeaking this problem down to calculations for a rod and calculations for a pipe. I hope to arrive at a formula that I can plug in the diameter of the conductor and wall thickness of the insulation.
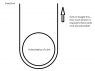
The pulley diameter is 3.43 meters
The Cable will bend 180 degrees around the pulley
This can be a static calculation... One end of cable may be assumed as fixed and the other being pulled until the cable forms snugly around the pulley.
Thanks for any help.
The pulley diameter is 3.43 meters
The Cable will bend 180 degrees around the pulley
This can be a static calculation... One end of cable may be assumed as fixed and the other being pulled until the cable forms snugly around the pulley.
Thanks for any help.