Bernoulli's equation and water exit speed from tank opening

[Derek1997]

Homework Statement

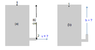
Use Bernoulli’s equation to calculate how fast the water emerges from the open tap (at position 2) in the figure(a). You may assume that the water at position 1 moves negligibly slowly
(b) The tap is rotated to create a fountain as shown in (b) Calculate the maximum height h that
the water could reach

Homework Equations

Bernoulli's equation

The Attempt at a Solution

Im looking to answer question b, I'm pretty sure I've done part A right.
So for B what I did was since I got v from part a which was 3.96, hence I did follow on the part from part a, that is= rho h1= 1/2 v^2 changing to solve for h, then I got h as 1.25 meters. Idk If i did part b right.

 

[Bystander]

Looks good based on what I can see ... I'll give you a conditional thumb's up. Haven't actually "crunched" the square root.

 

[gneill]

The image shows the tank's total height to be 80 cm. That's 0.80 m. How can the water from the "fountain" exceed that height? Sounds like a magnificent start for an over unity machine

 

[Bystander]

That's 0.80 m. How can the water from the "fountain" exceed that height?

Google "hydraulic ram water pump."

 

[gneill]

Google "hydraulic ram water pump."

The column of water above the tap inside the tank is not literally falling (except perhaps minutely due to the overall water level falling). So it doesn't carry momentum before suddenly hitting the exit port.The water is forced out by ambient pressure.

If this worked and the height of the jet of water ended up above the level of the tank, one could direct it to fall back into the tank. Perpetual motion would ensue, and you could extract energy by having it fall through a waterwheel on its way to the tank.

 

[Bystander]

If this worked and the height of the jet of water ended up above the level of the tank, one could direct

some of

it to fall back into the tank.

You are totally annihilating the water at the apex of its trajectory.

 

[Chestermiller]

I concur with gneill. Bernoulli will predict the height will be the same 80 cm as in the tank.

 

[Bystander]

Map the stream lines; I took the intuitive route initially, also.

 

[Chestermiller]

Map the stream lines; I took the intuitive route initially, also.

It's not intuitive. It's just straight application of the Bernoulli equation. It even gives the same result in the second part as just taking an initial upward velocity of $v_0$, and applying $v_f^2 = v_0^2-2gz$.

 

[Bystander]

Are you annihilating the water at the apex?

 

[Chestermiller]

Are you annihilating the water at the apex?

I assume that, by the apex, you mean the high point of the water spout. If that's the case, the answer is "no." Approaching this point, the streamlines diverge and then turn downward again (a little like an umbrella).

 

[Bystander]

diverge and then turn downward

Think about that.

 

[Chestermiller]

I guess we have a difference between experts here, and we are going to have to agree to disagree (unless someone else like @boneh3ad wants to chime in).

 

[lychette]

Google "hydraulic ram water pump."

211000 resposes...which one do you recommend? for this post

 

[Bystander]

Alternatively, Bernoulli isn't necessary --- one can simply look at the the difference in head heights, and declare that the static maximum difference (zero) is the maximum possible difference.

 

[gneill]

There's no reason why the nozzle of the outlet couldn't be angled a tad to allow the stream to form a parabolic arc that ended up over the tank. The tank height is only 80 cm above the nozzle, and some have predicted that the stream could reach 1.25 meters in height if directed straight up. Then:

I cannot justify this energetically. It would be akin to a ball bouncing higher than it falls.

 

[lychette]

I guess we have a difference between experts here, and we are going to have to agree to disagree (unless someone else like @boneh3ad wants to chime in).

'experts' ?? how many? between implies 2

 

[Bystander]

211000 resposes...which one do you recommend?

I've not found the one that raised my eyebrows twenty years ago, an open irrigation ditch, running downhill, and "magically" lifting two or three per cent of the flow to a height one or two feet greater than the source.

 

[lychette]

I've not found the one that raised my eyebrows twenty years ago, an open irrigation ditch, running downhill, and "magically" lifting two or three per cent of the flow to a height one or two feet greater than the source.

Ok thankyou

 

[Bystander]

stream to form a parabolic arc that ended up over the tank. The tank height is only 80 cm

... and the lateral motion comes from where?

It would be akin to a ball bouncing higher than it falls.

What about part of the ball? Have you never "splashed" a liquid?

 

[gneill]

... and the lateral motion comes from where?

It's just projectile motion. A bit of the vy is "stolen" to allow some vx. Apparently we have height to spare!

What about part of the ball? Have you never "splashed" a liquid?

Sure. But the whole volume of the tank is not "hitting" the tap opening to impart momentum in a collision with the water there. For a large tank the water is practically stagnant. A hydraulic ram takes advantage of the energy in a large quantity of moving water and sets up a "collision" that imparts momentum to a smaller quantity of water. Like a large mass hitting a small mass. But you need to have the momentum in the large mass of water prior to the "collision".

I maintain that if this phenomena were true for this non-flowing tank then we would have perpetual motion machines and over unity power generation as the tank water continuously cycled around the loop. The best you could hope for is to have the jet just reach the height of the surface water of the tank.

 

[Derek1997]

It's just projectile motion. A bit of the vy is "stolen" to allow some vx. Apparently we have height to spare!

Sure. But the whole volume of the tank is not "hitting" the tap opening to impart momentum in a collision with the water there. For a large tank the water is practically stagnant. A hydraulic ram takes advantage of the energy in a large quantity of moving water and sets up a "collision" that imparts momentum to a smaller quantity of water. Like a large mass hitting a small mass. But you need to have the momentum in the large mass of water prior to the "collision".

I maintain that if this phenomena were true for this non-flowing tank then we would have perpetual motion machines and over unity power generation as the tank water continuously cycled around the loop. The best you could hope for is to have the jet just reach the height of the surface water of the tank.

Hi i got 0.8 meters, is it right?

 

[Bystander]

You're going to have to give us the entire problem statement.

 

[Derek1997]

that's in page 1

 

[Bystander]

Orifice/tap dimensions/configurations?

 

[gneill]

Hi i got 0.8 meters, is it right?

Yes, that would be my conclusion.

I will be interested to see if a different result can be derived.

 

[Chestermiller]

Hi i got 0.8 meters, is it right?

Yes. This is the same thing as shooting a water hose into the air.

 

[boneh3ad]

I have to say that I agree with @gneill and @Chestermiller here. You will only get an energy density at the bottom of the tank that is equivalent to the hydrostatic pressure from the depth of the water, which is then converted entirely to velocity in the outlet. That kinetic energy at the outlet is then converted back into potential energy as it travels upward. Essentially, you are saying that it starts with hydrostatic pressure (potential energy) $\rho g h_1$, which is then converted to kinetic energy (dynamic pressure) $\frac{1}{2}\rho v^2$, and that is then converted back to potential energy $\rho g h_2$. If there are no losses, then that simply predicts that $h_1 = h_2$ and the heights are equal. Of course the real world has losses, but problems like this are typically assigned with the assumption of no losses in the flow as an illustration of energy conservation.

This also assumes the tank is sufficiently large as to be considered static inside. If the flow has some initial velocity, then that is an added source of kinetic energy, so you should, in theory, be able to squirt higher than the original surface.

 

[Bystander]

This also assumes the tank is sufficiently large as to be considered static inside. If the flow has some initial velocity, then that is an added source of kinetic energy, so you should, in theory, be able to squirt higher than the original surface.

 

[boneh3ad]

That is an example of water rushing into a mine, which contains a lot more kinetic energy in addition to gravitational potential than a tank with still water.