- #1
Timtam
- 42
- 0
I am trying to understand Bernoullis from Newton laws applied to molecular dynamics (as opposed to conservation laws)
From the conservation laws I understand for a incompressible invicous (experiencing no friction effects ) Ideal fluid
E= Dynamic Pressure + Static pressure + Potential Energy
If the datum is constant this reduces to
E= Dynamic Pressure + Static pressure
What I am trying to confirm is the Molecular Dynamics explanation of how these two energies are interchanged
My explanation for a streamline relies on the interactions between single molecule width 'sheets' of fluid along the streamline

As a fluid enters a reduction in pipe diameter the dynamic kinetic energy of a 'sheet' is shared via elastic collisions with the 'sheet' in front (or elastically with the walls of the pipe and back to the 'sheet' in front) .
As there are fewer molecules in the 'sheet' in front total kinetic energy is shared between a smaller denominator thus average energy (velocity) must increase.
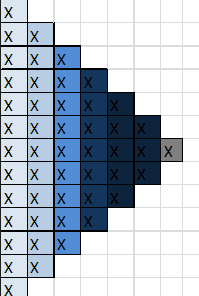
As each sheet has a higher velocity than its preceding neighbor it is accelerated away.
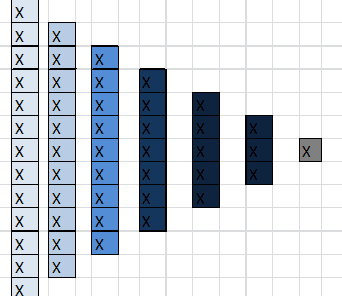
This acceleration means that the distance in front of the sheet is greater than the distance behind and the random kinetic motion experiences a positive bias (in mean free path / intermolecular forces ) in direction of the streamline thus also causing mean acceleration in that direction.
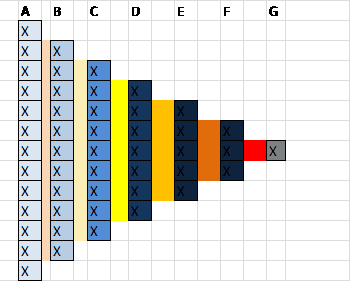
In summary Dynamic pressure increases and reducing Static pressure reduces thru a constriction is caused by the following sequential actions
1. Particle acceleration due to constant Dynamic Pressure energy being shared among a lower molecular denominator.
2. Static pressure being reduced as a result of a bias in mean free path / intromolecular forces in front of sheet vs behind
Is this correct ?
From the conservation laws I understand for a incompressible invicous (experiencing no friction effects ) Ideal fluid
- Mass is neither created nor destroyed Mass in = Mass Out
- Energy is neither created nor destroyed Energy in = Energy Out
- Energy is constant along the streamline
E= Dynamic Pressure + Static pressure + Potential Energy
If the datum is constant this reduces to
E= Dynamic Pressure + Static pressure
What I am trying to confirm is the Molecular Dynamics explanation of how these two energies are interchanged
My explanation for a streamline relies on the interactions between single molecule width 'sheets' of fluid along the streamline
As a fluid enters a reduction in pipe diameter the dynamic kinetic energy of a 'sheet' is shared via elastic collisions with the 'sheet' in front (or elastically with the walls of the pipe and back to the 'sheet' in front) .
As there are fewer molecules in the 'sheet' in front total kinetic energy is shared between a smaller denominator thus average energy (velocity) must increase.
As each sheet has a higher velocity than its preceding neighbor it is accelerated away.
This acceleration means that the distance in front of the sheet is greater than the distance behind and the random kinetic motion experiences a positive bias (in mean free path / intermolecular forces ) in direction of the streamline thus also causing mean acceleration in that direction.
In summary Dynamic pressure increases and reducing Static pressure reduces thru a constriction is caused by the following sequential actions
1. Particle acceleration due to constant Dynamic Pressure energy being shared among a lower molecular denominator.
2. Static pressure being reduced as a result of a bias in mean free path / intromolecular forces in front of sheet vs behind
Is this correct ?