Biot-Savart - Differential Length Element?

[nickypoo]

Hi, I'm trying to work with the Biot-Savart law to look at the magnetic field strength along the center of an asymmetric solenoid I wrapped.

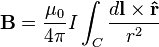
I parameterized the coils with x = r cos 2(pi)t, y = r sin 2(pi)t, and z = D t
where r is the radius of the coil layer, D is the diameter of the wire, and t represents the number of coils.

I'm having difficulty understanding what the "differential current length element" (dl) is in the equation. I understand the vector will be in the direction of the tangential velocity, but I don't understand the "differential" part.

Every other component in the equation is pretty straightforward to me.

First I tried dividing the unit vector of the velocity by the length of the curve, but I'm fairly certain that's just wrong. Pardon my ignorance. But I carried out the formula to completion with this and got a cool 2-dimensional function that had an accurately shaped graph, but inaccurate values.

Please help me understand what the "differential length" means. Would it just be the unit vector of the direction of current flow?

Thank you.

 

[nickypoo]

Well, I think I've found an answer by bumbling around for a little bit. If I use the velocity vector alone as dl then I get a solution that's exactly equivalent to a formula I found online for this calculation.

Now can anyone explain how this works?

Thank you.

 

[nickypoo]

Now I understand if I look at what I have to do to calculate the length of the curve. All the "differential length element" is, is the derivative of the length of the curve multiplied by the unit vector of velocity:

$\sqrt{(\frac{\partial x}{\partial t})^2+(\frac{\partial y}{\partial t})^2+(\frac{\partial z}{\partial t})^2}$ $\bullet$ $\hat{v}$


Or simply just the velocity vector.


Thanks for nothing! Lol jk.

 

[lavinia]

IdL is the current in the element of the wire dL. All you are doing is integrating the magnetic field that these current elements produce at a fixed point in space. This gives you the magnetic field that wire produces as the the sum of the fields produced by each element.

If I is measured as a current density, current/unit length, the dl must be the unit tangent.